如图，在平面直角坐标系 $xOy$ 中，抛物线 $C:y=-\dfrac 12x^2+4$ 与 $x$ 轴相交于 $A,B$ 两点，顶点为 $D$，设点 $F(m,0)$ 是 $x$ 轴的正半轴上一点，将抛物线 $C$ 绕点 $F$ 旋转 $180^\circ$，得到新的抛物线 $C'$，$P$ 是第一象限内抛物线 $C$ 上一点，它到两坐标轴的距离相等，点 $P$ 在抛物线 $C'$ 上的对应点为 $P'$，设 $M$ 是 $C$ 上的动点，$N$ 是 $C'$ 上的动点，试探究四边形 $PMP'N$ 能否成为正方形，若能，求出 $m$ 的值；若不能，请说明理由．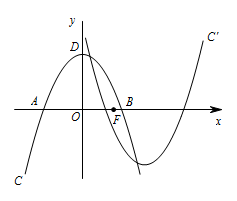
【难度】
【出处】
无
【标注】
【答案】
能，$m=4,6$ 或 $\sqrt {17}-3$
【解析】
设点 $P(a,b)$ 到两坐标轴距离相等，
所以 $|b|=\left|-\dfrac 12a^2+4\right|=|a|$，
因为点 $P$ 在第一象限，所以 $-\dfrac 12a^2+4=a$，解得 $a_1=2,a_2=-4$（舍）
所以点 $P(2,2)$，由中心对称型的点 $P'(2m-2,-2)$，
因为四边形 $PMP'N$ 是正方形，
所以点 $M$ 和点 $N$ 应关于点 $F$ 称中心对称，
过点 $M$ 作平行于 $y$ 轴，垂直于 $x$ 轴的垂线 $MG$，
过点 $P$ 作 $PG\perp MG$ 于点 $G$，
过点 $N$ 作平行于 $x$ 轴，垂直于 $y$ 轴的垂线 $NH$，
过点 $P'$ 作 $PH\perp MH$ 于点 $H$，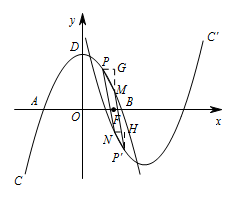
若四边形 $PMP'N$ 为正方形，则 $\triangle PMP'$ 为等腰直角三角形，
所以 $\triangle PGM\cong \triangle P'HM$，
所以 $PG=P'H,GM=MH$，
设点 $M(x,-\dfrac 12x^2+4)$，
所以 $\begin{cases}|x-2|=\left|-2-\left(-\dfrac 12x^2+4\right)\right|,\\ \left|2-\left(-\dfrac 12x^2+4\right)\right|=|2m-2-x|.\end{cases}$
① 当 $x<2$ 时，解得 $x=-2,m=0$（舍），
② 当 $2\leqslant x<2\sqrt 3$ 时，解得 $x=\sqrt{17}-1,m=4$ 或 $m=\sqrt{17}-3$，
③ 当 $2\sqrt 3\leqslant x$ 时，解得 $x=4,m=6$，
所以当 $m=4$ 或 $6$ 或 $\sqrt {17}-3$ 时四边形 $PMP'N$ 是正方形．
所以 $|b|=\left|-\dfrac 12a^2+4\right|=|a|$，
因为点 $P$ 在第一象限，所以 $-\dfrac 12a^2+4=a$，解得 $a_1=2,a_2=-4$（舍）
所以点 $P(2,2)$，由中心对称型的点 $P'(2m-2,-2)$，
因为四边形 $PMP'N$ 是正方形，
所以点 $M$ 和点 $N$ 应关于点 $F$ 称中心对称，
过点 $M$ 作平行于 $y$ 轴，垂直于 $x$ 轴的垂线 $MG$，
过点 $P$ 作 $PG\perp MG$ 于点 $G$，
过点 $N$ 作平行于 $x$ 轴，垂直于 $y$ 轴的垂线 $NH$，
过点 $P'$ 作 $PH\perp MH$ 于点 $H$，
若四边形 $PMP'N$ 为正方形，则 $\triangle PMP'$ 为等腰直角三角形，所以 $\triangle PGM\cong \triangle P'HM$，
所以 $PG=P'H,GM=MH$，
设点 $M(x,-\dfrac 12x^2+4)$，
所以 $\begin{cases}|x-2|=\left|-2-\left(-\dfrac 12x^2+4\right)\right|,\\ \left|2-\left(-\dfrac 12x^2+4\right)\right|=|2m-2-x|.\end{cases}$
① 当 $x<2$ 时，解得 $x=-2,m=0$（舍），
② 当 $2\leqslant x<2\sqrt 3$ 时，解得 $x=\sqrt{17}-1,m=4$ 或 $m=\sqrt{17}-3$，
③ 当 $2\sqrt 3\leqslant x$ 时，解得 $x=4,m=6$，
所以当 $m=4$ 或 $6$ 或 $\sqrt {17}-3$ 时四边形 $PMP'N$ 是正方形．
答案
解析
备注
