如图,过原点的直线 $y=k_1x$ 和 $y=k_2x$ 与反比例函数 $y=\dfrac{1}{x}$ 的图象分别交于两点 $A,C$ 和 $B,D$,连接 $AB,BC,CD,DA$.四边形 $ABCD$ 可能是矩形吗?若可能,试求此时 $k_1$ 和 $k_2$ 之间的关系式;若不可能,说明理由.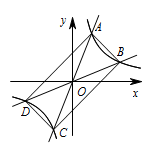

【难度】
【出处】
无
【标注】
【答案】
四边形 $ABCD$ 能是矩形,此时 $k_{1}k_{2}=1$
【解析】
因为直线 $y=k_{1}x$ 和 $y=k_{2}x$ 与反比例函数 $y=\dfrac 1x$ 的图象关于原点对称,
所以 $ OA=OC$,$OB=OD$,
所以四边形 $ABCD$ 是平行四边形.
联立方程组 $\begin{cases}y=k_1x,\\y=\dfrac{1}{x},\end{cases}$
解得 $\begin{cases}x_1=\sqrt{\dfrac{1}{k_1}},\\y_1=\sqrt{k_1},\end{cases}\begin{cases}x_2=-\sqrt{\dfrac{1}{k_1}},\\y_2=-\sqrt{k_1}.\end{cases}$
故点 $A$ 的坐标为 $\left(\sqrt{\dfrac{1}{k_1}},\sqrt{k_1}\right)$.
同理可得点 $B$ 坐标为 $\left(\sqrt{\dfrac{1}{k_2}},\sqrt{k_2}\right)$,
若四边形 $ABCD$ 是矩形,则 $OA=OB$,
所以 $\sqrt{\dfrac{1}{k_1}+k_1}=\sqrt{\dfrac{1}{k_2}+k_2}$,
整理后得 $\left(k_{1}-k_{2}\right)\left(k_{1}k_{2}-1\right)=0$,
而 $k_{1}\neq k_{2}$,
所以 $k_{1}k_{2}-1=0$,即 $k_{1}k_{2}=1$.
综上可得,四边形 $ABCD$ 能是矩形,此时 $k_{1}k_{2}=1$.
所以 $ OA=OC$,$OB=OD$,
所以四边形 $ABCD$ 是平行四边形.
联立方程组 $\begin{cases}y=k_1x,\\y=\dfrac{1}{x},\end{cases}$
解得 $\begin{cases}x_1=\sqrt{\dfrac{1}{k_1}},\\y_1=\sqrt{k_1},\end{cases}\begin{cases}x_2=-\sqrt{\dfrac{1}{k_1}},\\y_2=-\sqrt{k_1}.\end{cases}$
故点 $A$ 的坐标为 $\left(\sqrt{\dfrac{1}{k_1}},\sqrt{k_1}\right)$.
同理可得点 $B$ 坐标为 $\left(\sqrt{\dfrac{1}{k_2}},\sqrt{k_2}\right)$,
若四边形 $ABCD$ 是矩形,则 $OA=OB$,
所以 $\sqrt{\dfrac{1}{k_1}+k_1}=\sqrt{\dfrac{1}{k_2}+k_2}$,
整理后得 $\left(k_{1}-k_{2}\right)\left(k_{1}k_{2}-1\right)=0$,
而 $k_{1}\neq k_{2}$,
所以 $k_{1}k_{2}-1=0$,即 $k_{1}k_{2}=1$.
综上可得,四边形 $ABCD$ 能是矩形,此时 $k_{1}k_{2}=1$.
答案
解析
备注