在平 面直角坐标系中，$O$ 为原点，直线 $y =-2x-1$ 与 $y$ 轴交于点 $A$，与 直线 $y =-x$ 交于点 $B$，点 $B$ 关于 原点的对称点为点 $C$．$P$ 为抛物线上一点，它关于原点的对称点为 $Q$．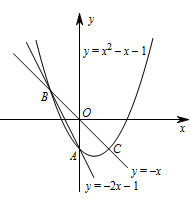
【难度】
【出处】
无
【标注】
-
当四边形 $PBQC$ 为菱形时，求点 $P$ 的坐标；标注答案点 $P$ 的坐标为 $\left(1+\sqrt 2,1+\sqrt 2\right)$ 或 $\left(1-\sqrt 2,1-\sqrt 2\right)$解析解方程组 $\begin{cases}y=-2x-1, \\ y=-x,\end{cases}$ 得 $\begin{cases} x=-1, \\ y=1.\end{cases}$
所以点 $B$ 的坐标为 $\left(-1,1\right)$．
因为点 $C$ 和点 $B$ 关于原点对称，
所以点 $C$ 的坐标为 $\left(1,-1\right)$．
因为点 $A$ 是直线 $y=-2x-1$ 与 $y$ 轴的交点，
所以点 $A$ 的坐标为 $\left(0,-1\right)$．
设抛物线的解析式为 $y=ax^2+bx+c$，
所以 $\begin{cases}a-b+c=1 , \\ a+b+c=-1 ,\\ c=-1,\end{cases}$ 解得 $\begin{cases} a=1,\\ b=-1, \\ c=-1.\end{cases}$
所以抛物线的解析式为 $y=x^2-x-1$．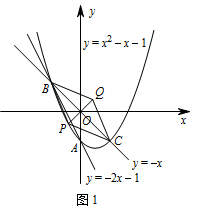
如图1，因为点 $P$ 在抛物线上，
所以可设点 $P$ 的坐标为 $\left(m,m^2-m-1\right)$．
当四边形 $PBQC$ 是菱形时，$O$ 为菱形的中心，
所以 $PQ\perp BC$，即点 $P$，$Q$ 在直线 $y=x$ 上，
所以 $m=m^2-m-1$，解得 $m=1\pm \sqrt 2$．
所以点 $P$ 的坐标为 $\left(1+\sqrt 2,1+\sqrt 2\right)$ 或 $\left(1-\sqrt 2,1-\sqrt 2\right)$． -
若点 $P$ 的横坐标为 $t\left(-1<t<1\right)$，当 $t$ 为何值时，四边形 $PBQC$ 面积最大，并说明理由．标注答案当 $t=0$ 时，四边形 $PBQC$ 面积最大，最大值为 $2$解析
解法一 如图 2，设点 $P$ 的坐标为 $\left(t,t^2-t-1\right)$．
过点 $P$ 作 $PD \parallel y$ 轴，交直线 $y=-x$ 于点 $D$，则点 $D\left(t,-t\right)$．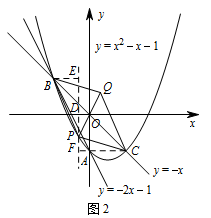
分别过点 $B,C$ 作 $BE\perp PD,CF\perp PD$，垂足分别为点 $E,F$．
所以 $PD=-t-\left(t^2-t-1\right)=-t^2+1$，$BE+CF=2$，
$\begin{split}\text{所以}S_{\triangle PBC}&=\dfrac 12PD\cdot BE+\dfrac 12PD\cdot CF \\&=\dfrac 12PD\cdot \left(BE+CF\right) \\&=\dfrac 12\left(-t^2+1\right)\times 2\\&=-t^2+1.\end{split}$
所以 $S_{\text{四边形}PBQC}=-2t^2+2$．
所以当 $t=0$ 时，$S_{\text{四边形}PBQC}$ 有最大值 $2$．解法二 如图 3，过点 $B$ 作 $y$ 轴的平行线，过点 $C$ 作 $x$ 轴的平行线，两直线交于点 $D$，连接 $PD$．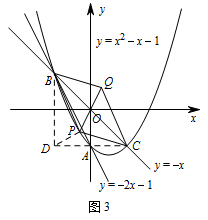
$\begin{split}\text{所以}S_{\triangle PBC}&=S_{\triangle BDC}-S_{\triangle PBD}-S_{\triangle PDC} \\&=\dfrac 12\times 2\times 2-\dfrac 12\times 2\left(t+1\right)-\dfrac 12\times 2\left(t^2-t-1+1\right) \\&=-t^2+1.\end{split}$
所以 $S_{\text{四边形}PBQC}=-2t^2+2$．
所以当 $t=0$ 时，$S_{\text{四边形}PBQC}$ 有最大值 $2$．解法三 如图 4，过点 $P$ 作 $PE\perp BC$，垂足为 $E$．
作 $PF\parallel x$ 轴交 $BC$ 于点 $F$．所以 $PE=EF$．
因为点 $P$ 的坐标为 $\left(t,t^2-t-1\right)$，
所以点 $F$ 的坐标为 $\left(-t^2+t+1, t^2-t-1\right)$．
所以 $PF=-t^2+t+1-t =-t^2+1$．
所以 $S_{\triangle PBC}=\dfrac 12BC\cdot PE=\dfrac 12\times 2\sqrt 2\times \dfrac {\sqrt 2}{2}\left(-t^2+1\right)=-t^2+1$．
所以 $S_{\text{四边形}PBQC}=-2t^2+2$．
所以当 $t=0$ 时，$S_{\text{四边形}PBQC}$ 有最大值 $2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
