在平面直角坐标系 $xOy$ 中的点 $P$ 和图形 $M$，给出如下的定义：若在图形 $M$ 上存在一点 $Q$，使得 $P,Q$ 两点间的距离小于或等于 $1$，则称 $P$ 为图形 $M$ 的关联点．
【难度】
【出处】
无
【标注】
-
当 $\odot O$ 的半径为 $2$ 时，点 $P$ 在直线 $y=-x$ 上，若 $P$ 为 $\odot O$ 的关联点，求点 $P$ 的横坐标的取值范围；标注答案点 $P$ 的横坐标为 $-\dfrac{3\sqrt 2}2\leqslant x\leqslant -\dfrac{\sqrt 2}2$ 或 $\dfrac{\sqrt 2}2\leqslant x\leqslant \dfrac{3\sqrt 2}2$解析如图，分别以 $1,3$ 个单位长度为半径作 $\odot O$，令直线 $y=-x$ 与两圆的交点为 $P_1,P_2,P_3,P_4$，则 $OP_1=OP_2=3$，$OP_3=OP_4=1$．
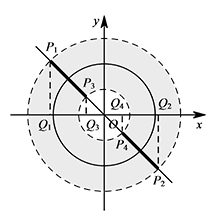分别过点 $P_1,P_2,P_3,P_4$ 作 $x$ 轴的垂线，垂足为 $Q_1,Q_2,Q_3,Q_4$，
易得 $OQ_1=OQ_2=\dfrac{3\sqrt 2}2$，$OQ_3=OQ_4=\dfrac{\sqrt 2}2$．
从图中可以看出线段 $P_1P_3,P_2P_4$ 上的点均为 $\odot O$ 的关联点，
所以点 $P$ 的横坐标为 $-\dfrac{3\sqrt 2}2\leqslant x\leqslant -\dfrac{\sqrt 2}2$ 或 $\dfrac{\sqrt 2}2\leqslant x\leqslant \dfrac{3\sqrt 2}2$． -
$\odot C$ 的圆心在 $x$ 轴上，半径为 $2$，直线 $y=-x+1$ 与 $x$ 轴、$y$ 轴交于点 $A,B$．若线段 $AB$ 上的所有点都是 $\odot C$ 的关联点，求圆心 $C$ 的横坐标的取值范围．标注答案圆心 $C$ 的横坐标的取值范围为 $-2\leqslant x\leqslant 1-\sqrt 2$ 或 $2\leqslant x\leqslant 2\sqrt 2$解析易得点 $A(1,0)$，点 $B(0,1)$．
分别以 $1,3$ 个单位长度为半径作 $\odot C$，则两圆构成的圆环内的所有点（包括边界）均为半径为 $2$ 的 $\odot C$ 的关联点．
圆心 $C$ 从左往右移动的过程中：
① 如图，当圆心 $C$ 在 $AB$ 左侧且圆环外边界过点 $A$ 时．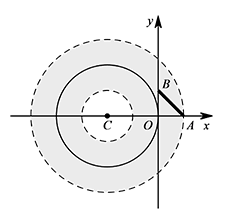
则 $CA=3$，此时圆心 $C$ 的坐标为 $(-2,0)$；
② 如图，当圆心 $C$ 在 $AB$ 左侧且圆环内边界与 $AB$ 相切于点 $D$ 时．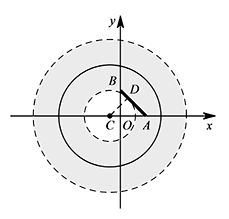
连接 $CD$，易得 $AD=CD=1$，所以 $AC=\sqrt 2$，
此时圆心 $C$ 的坐标为 $(1-\sqrt 2,0)$；
③ 如图，当圆心 $C$ 在 $AB$ 右侧且圆环内边界过点 $A$ 时．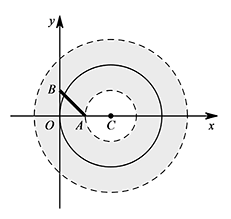
则 $CA=1$，此时圆心 $C$ 的坐标为 $(2,0)$；
④ 如图，当圆心 $C$ 在 $AB$ 右侧且圆环外边界过点 $B$ 时．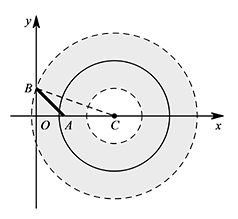
连接 $CB$，则 $CB=3$．
所以 $OC=\sqrt{CB^2-BO^2}=2\sqrt 2$，
此时圆心 $C$ 的坐标为 $(2\sqrt 2,0)$．
结合图形，圆心 $C$ 的横坐标的取值范围为 $-2\leqslant x\leqslant 1-\sqrt 2$ 或 $2\leqslant x\leqslant 2\sqrt 2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
