如图，抛物线 $y = - {x^2} + 2x + 3$ 与 $x$ 轴交与 $A$，$B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$．点 $D$ 和点 $C$ 关于抛物线的对称轴对称，直线 $AD$ 与 $y$ 轴相交于点 $E$．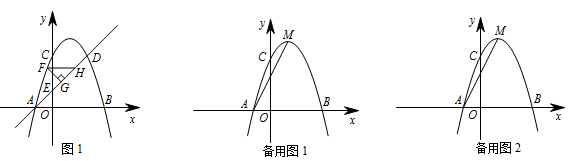
【难度】
【出处】
无
【标注】
-
如图 1，直线 $AD$ 上方的抛物线上有一点 $F$，过点 $F$ 作 $FG\perp AD$ 于点 $G$，作 $FH$ 平行于 $x$ 轴交直线 $AD$ 于点 $H$，求 $\triangle FGH$ 的周长的最大值；标注答案最大周长为 $\dfrac{9 + 9\sqrt 2 }{4}$解析令 $ - {x^2} + 2x + 3=0$，解得 $ x_1=-1 $、$ x_2=3 $，
所以 $ A\left(-1,0\right)$．
令 $ x=0 $，$y=3 $．
所以 $ C\left(0,3\right)$．
对称轴 $x=1$，
所以 $ D\left(2,3\right) $．
直线 $AD$ 的解析式为 $y = x + 1$．
过点 $F$ 作 $x$ 轴的垂线，交直线 $AD$ 于点 $M$，
显然 $\angle FHA=\angle DAB=45^\circ $，
所以 $ \triangle FGH\cong \triangle FGM$，
故 ${C_{\triangle FGH}} = {C_{\triangle FGM}}$．
设 $F\left(m, - {m^2} + 2m + 3\right)$，
则 $FM= - {m^2} + 2m + 3 - \left(m + 1\right) = - {m^2} + m + 2$，
则 $C= FM + 2 \times \dfrac{FM}{\sqrt 2 } = \left(1 + \sqrt 2 \right)FM = - \left(1 + \sqrt 2 \right){\left(m - \dfrac{1}{2}\right)^2} + \dfrac{9 + 9\sqrt 2 }{4}$．
故最大周长为 $\dfrac{9 + 9\sqrt 2 }{4}$． -
点 $M$ 是抛物线的顶点，点 $P$ 是 $y$ 轴上一点，点 $Q$ 是坐标平面内一点，以 $A$，$M$，$P$，$Q$ 为顶点的四边形是 $AM$ 为边的矩形，若点 $T$ 和点 $Q$ 关于 $AM$ 所在直线对称，求点 $T$ 的坐标．标注答案点 $ T $ 坐标为 $\left(0,\dfrac{9}{2}\right)$解析① 若 $AP$ 为对角线，如图．
由 $\triangle PMS\backsim \triangle MAR$ 可得 $P\left(0,\dfrac{9}{2}\right)$．
由点的平移可知 $Q\left(-2,\dfrac 12\right)$．
故 $Q$ 点关于直线 $AM$ 的对称点 $T$ 为 $\left(0, - \dfrac{1}{2}\right)$；
② 若 $ AQ $ 为对角线，如图．
同理可知 $P\left(0, - \dfrac{1}{2}\right)$．
由点的平移可知 $Q \left(2,\dfrac{7}{2}\right)$．
故 $Q$ 点关于直线 $AM$ 的对称点 $ T $ 为 $\left(0,\dfrac{9}{2}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
