如图，在平面直角坐标系 $xOy$ 中，抛物线 $y=ax^2-2ax-3a\left(a<0\right)$ 与 $x$ 轴交于 $A,B$ 两点（点 $A$ 在点 $B$ 的左侧），经过点 $A$ 的直线 $l$：$y=ax+a$ 与抛物线的另一个交点为 $C$．设 $P$ 是抛物线的对称轴上的一点，点 $Q$ 在抛物线上，以点 $A,C,P,Q$ 为顶点的四边形能否成为矩形？若能，求出点 $P$ 的坐标；若不能，请说明理由．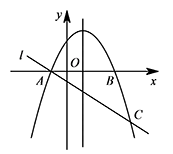
【难度】
【出处】
无
【标注】
【答案】
能，点 $P$ 的坐标为 $\left(1,-\dfrac {26\sqrt 7}{7}\right)$ 或 $\left(1,-4\right)$
【解析】
以点 $A,C,P,Q$ 为顶点的四边形能成为矩形．
令 $ax^2-2ax-3a=ax+a$，解得 $x_{1}=-1$，$x_{2}=4$，
所以点 $A$ 的坐标为 $(-1,0)$，点 $C$ 的坐标为 $\left(4,5a\right)$．
因为 $y=ax^2-2ax-3a$，所以抛物线的对称轴为 $x=1$，则 $x_P=1$．
① 若 $AC$ 是矩形的一条边，如图．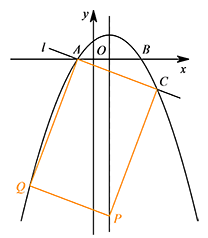
则 $x_A+x_P=x_C+x_Q$，可得 $x_Q=-4$，从而点 $Q$ 的坐标为 $(-4,21a)$．
同样 $y_A+y_P=y_C+y_Q$，可得 $y_P=26a$，从而点 $P$ 的坐标为 $(1,26a)$．
因为 $AP=CQ$，所以有 $2^2+(26a)^2=8^2+(16a)^2$，
解得 $a_1=-\dfrac{\sqrt 7}7$，$a_2=\dfrac{\sqrt 7}7$（舍），
所以此时点 $P$ 的坐标为 $\left(1,-\dfrac{26\sqrt 7}7\right)$．
② 若 $AC$ 是矩形的一条对角线，如图．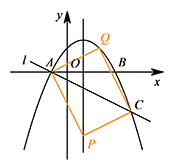
则 $x_A+x_C=x_P+x_Q$，可得 $x_Q=2$，从而点 $Q$ 的坐标为 $(2,-3a)$．
同样 $y_A+y_C=y_P+y_Q$，可得 $y_P=8a$，从而点 $P$ 的坐标为 $(1,8a)$．
因为 $AC=PQ$，所以有 $5^2+(5a)^2=1^2+(11a)^2$，
解得 $a_1=-\dfrac 12$，$a_2=\dfrac 12$（舍），
所以此时点 $P$ 的坐标为 $(1,-4)$．
综上所得，以点 $A,C,P,Q$ 为顶点的四边形能成为矩形，点 $P$ 的坐标为 $\left(1,-\dfrac {26\sqrt 7}{7}\right)$ 或 $\left(1,-4\right)$．
令 $ax^2-2ax-3a=ax+a$，解得 $x_{1}=-1$，$x_{2}=4$，
所以点 $A$ 的坐标为 $(-1,0)$，点 $C$ 的坐标为 $\left(4,5a\right)$．
因为 $y=ax^2-2ax-3a$，所以抛物线的对称轴为 $x=1$，则 $x_P=1$．
① 若 $AC$ 是矩形的一条边，如图．
则 $x_A+x_P=x_C+x_Q$，可得 $x_Q=-4$，从而点 $Q$ 的坐标为 $(-4,21a)$．同样 $y_A+y_P=y_C+y_Q$，可得 $y_P=26a$，从而点 $P$ 的坐标为 $(1,26a)$．
因为 $AP=CQ$，所以有 $2^2+(26a)^2=8^2+(16a)^2$，
解得 $a_1=-\dfrac{\sqrt 7}7$，$a_2=\dfrac{\sqrt 7}7$（舍），
所以此时点 $P$ 的坐标为 $\left(1,-\dfrac{26\sqrt 7}7\right)$．
② 若 $AC$ 是矩形的一条对角线，如图．
则 $x_A+x_C=x_P+x_Q$，可得 $x_Q=2$，从而点 $Q$ 的坐标为 $(2,-3a)$．同样 $y_A+y_C=y_P+y_Q$，可得 $y_P=8a$，从而点 $P$ 的坐标为 $(1,8a)$．
因为 $AC=PQ$，所以有 $5^2+(5a)^2=1^2+(11a)^2$，
解得 $a_1=-\dfrac 12$，$a_2=\dfrac 12$（舍），
所以此时点 $P$ 的坐标为 $(1,-4)$．
综上所得，以点 $A,C,P,Q$ 为顶点的四边形能成为矩形，点 $P$ 的坐标为 $\left(1,-\dfrac {26\sqrt 7}{7}\right)$ 或 $\left(1,-4\right)$．
答案
解析
备注
