如图，在平面直角坐标系 $xOy$ 中，抛物线 $y = a{\left( {x + 1} \right)^2} - 3$ 与 $x$ 轴交于 $A$，$B$ 两点（点 $A$ 在点 $B$ 左侧），与 $y$ 轴交于点 $C\left(0,-\dfrac{8}{3} \right)$，顶点为 $D$，对称轴与 $x$ 轴交于点 $H$．过点 $H$ 的直线 $l$ 交抛物线于 $P,Q$ 两点，点 $Q$ 在 $y$ 轴右侧．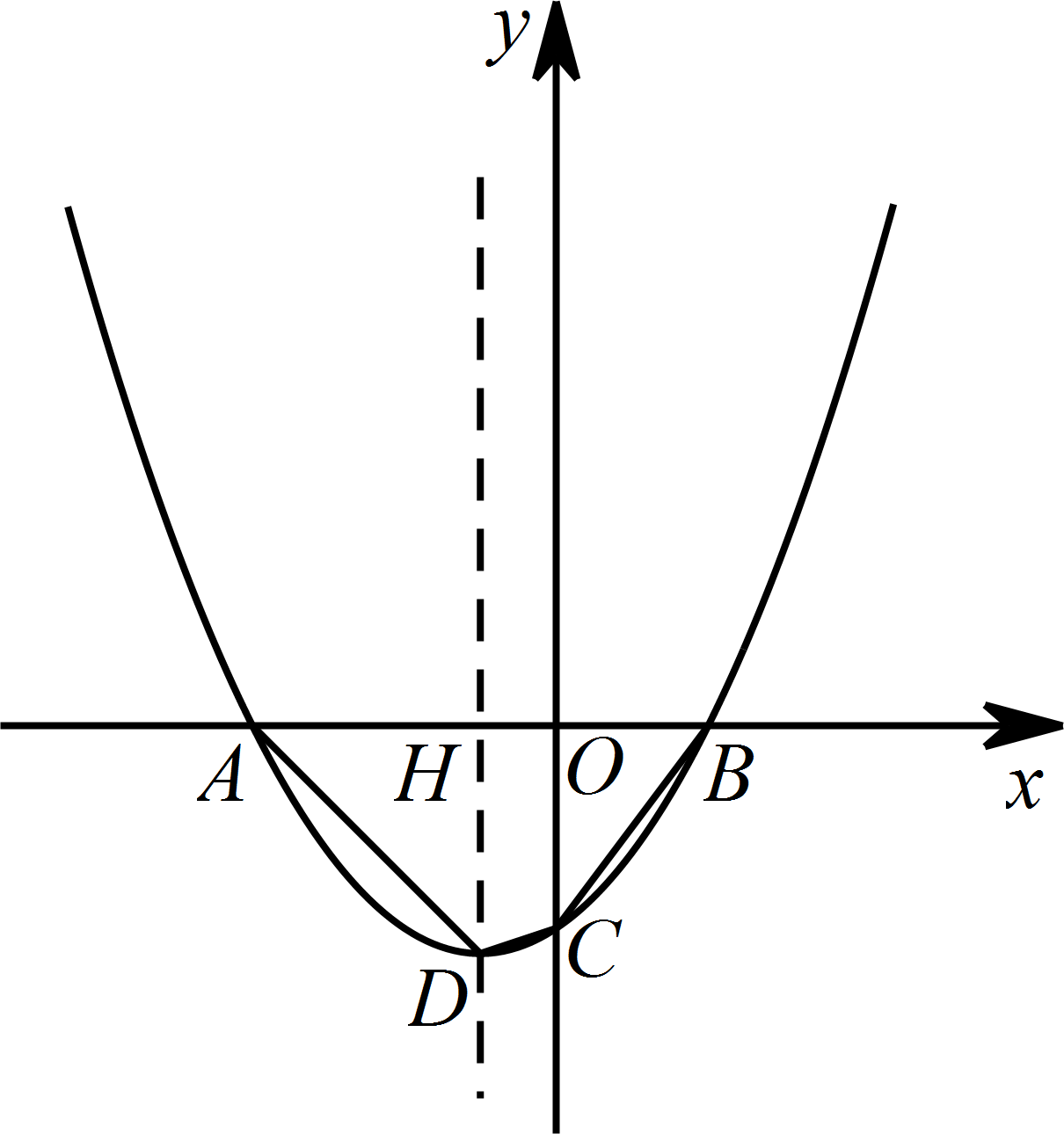
【难度】
【出处】
无
【标注】
-
当直线 $l$ 将四边形 $ABCD$ 分为面积比为 $3:7$ 的两部分时，求直线 $l$ 的函数表达式；标注答案直线 $l$ 的函数表达式为 $y=2x+2$ 或 $y=-\dfrac{4}{3}x-\dfrac{4}{3}$解析因为抛物线 $y = a{\left( {x + 1} \right)^2}-3$ 与 $y$ 轴交于点 $C\left(0,-\dfrac{8}{3}\right)$．
所以 $a-3=-\dfrac{8}{3}$，即 $a=\dfrac{1}{3}$，
所以抛物线的解析式为 $y=\dfrac{1}{3}\left(x+1\right)^{2}-3$．
当 $y=0$ 时，有 $\dfrac{1}{3}\left(x+1\right)^{2}-3=0$，
解得 $x_{1}=2$，$x_{2}=-4$，
所以点 $A\left(-4,0\right)$，点 $B\left(2,0\right)$．
$\begin{split}
\text{所以}S_{四边形ABCD}&=S_{\triangle AHD}+S_{梯形OCDH}+S_{\triangle BOC}\\
&= \dfrac{1}{2}\times 3\times 3+\dfrac{1}{2}\left(\dfrac{8}{3}+ 3\right) \times 1+\dfrac{1}{2}\times 2\times \dfrac{8}{3}\\
&=10.\end{split}$
从面积分析知，直线 $l$ 只能与边 $AD$ 或 $BC$ 相交，所以有两种情况：
① 当直线 $l$ 边 $AD$ 相交与点 $M_{1}$ 时，则 $S_{\triangle AHM1}=\dfrac{3}{10}\times 10=3$，
所以 $\dfrac{1}{2}\times 3\times \left(-y_{M1}\right)=3$，
所以 $y_{M1}=-2$，即点 $M_{1}\left(-2,-2\right)$，
所以过点 $H\left(-1,0\right)$ 和 $M_{1}\left(-2,-2\right)$ 的直线 $l$ 的解析式为 $y=2x+2$．
② 当直线 $l$ 边 $BC$ 相交与点 $M_{2}$ 时，同理可得点 $M_{2}\left(\dfrac{1}{2},-2\right)$，
所以过点 $H\left(-1,0\right)$ 和 $M_{2}\left(\dfrac{1}{2},-2\right)$ 的直线 $l$ 的解析式为 $y=-\dfrac{4}{3}x-\dfrac{4}{3}$．
综上所述，直线 $l$ 的函数表达式为 $y=2x+2$ 或 $y=-\dfrac{4}{3}x-\dfrac{4}{3}$． -
当点 $P$ 位于第二象限时，设 $PQ$ 的中点为 $M$，点 $N$ 在抛物线上，则以 $DP$ 为对角线的四边形 $DMPN$ 能否成为菱形？若能，求出点 $N$ 的坐标；若不能，请说明理由．标注答案以 $DP$ 为对角线的四边形 $DMPN$ 能成为菱形，此时点 $N$ 的坐标为 $\left(-2\sqrt 3-1, 1\right)$解析设过点 $H\left(-1,0\right)$ 的直线 $PQ$ 的解析式为 $y=kx+b$，
所以 $-k+b=0$，即 $k=b$．
所以直线 $PQ$ 为 $y=kx+k$．
设点 $P\left(x_{1},y_{1}\right)$，点 $Q\left(x_{2},y_{2}\right)$．
由 $\begin{cases}
y=kx + k,\\
y=\dfrac{1}{3}{x^2} + \dfrac{2}{3}x - \dfrac{8}{3},\\
\end{cases}$
得 $\dfrac{1}{3}{x^2} + \left(\dfrac{2}{3} - k\right)x - \dfrac{8}{3} - k = 0$，
所以 $x_{1}+x_{2}=-2+3k$，$y_{1}+y_{2}=kx_{1}+k+kx_{2}+k=3k^{2}$，
因为点 $M$ 是线段 $PQ$ 的中点，
所以由中点坐标公式的点 $M\left(\dfrac{3}{2}k-1,\dfrac{3}{2}k^{2}\right)$．
假设存在这样的 $N$ 点如下图，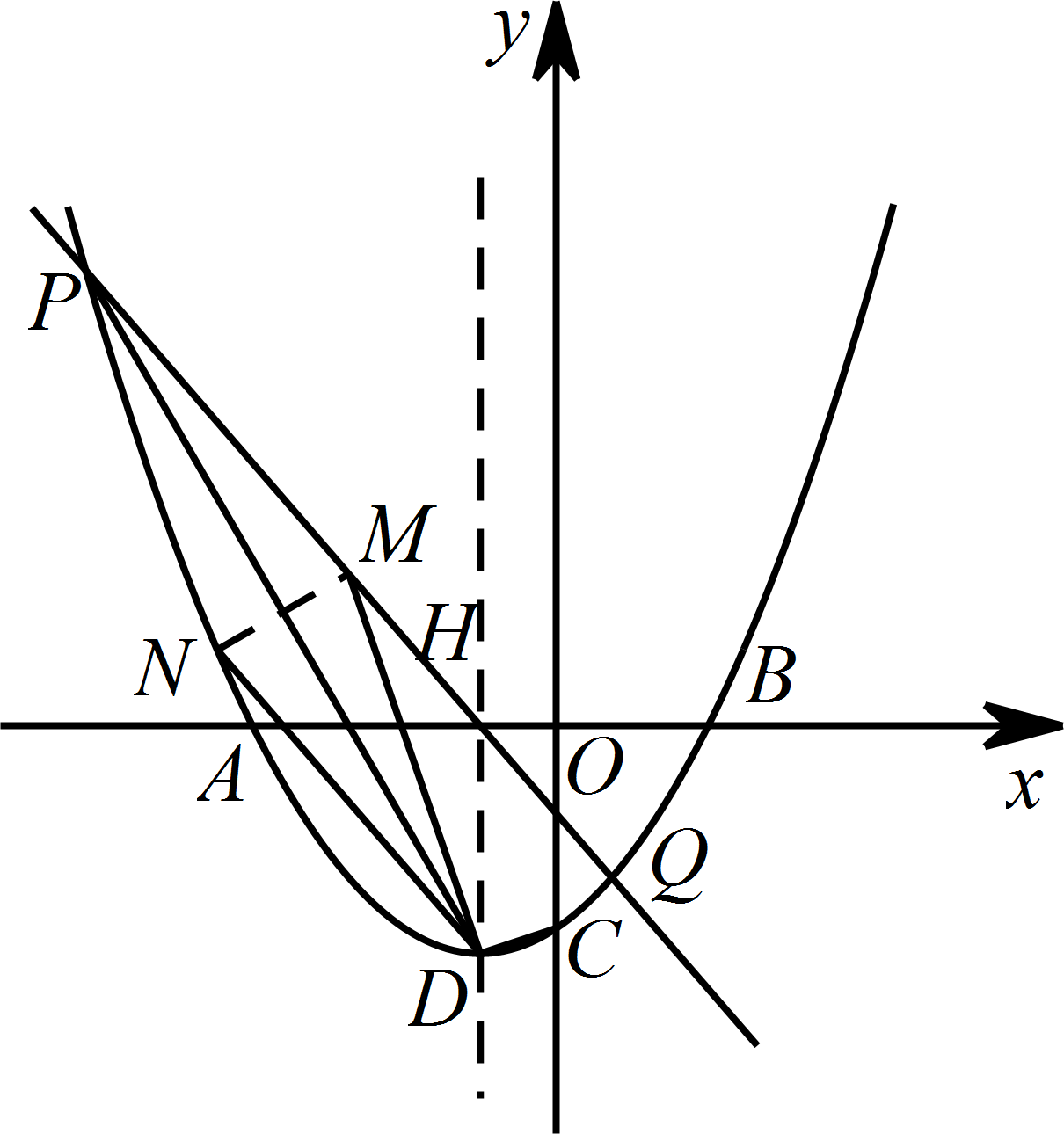
直线 $DN\parallel PQ$，设直线 $DN$ 的解析式为 $y=kx+k-3$，
由 $\begin{cases}
y = kx + k - 3,\\
y = \dfrac{1}{3}{x^2} + \dfrac{2}{3}x - \dfrac{8}{3},\\
\end{cases}$
解得 $x_{1}=-1, x_{2}=3k-1$，
所以点 $N\left(3k-1,3k^{2}-3\right)$．
因为四边形 $DMPN$ 是菱形，所以 $DN=DM$，
所以 $ {\left(3k\right)^2} + {\left(3{k^2}\right)^2} = {\left(\dfrac{3k}{2}\right)^2} + {\left(\dfrac{3}{2}{k^2} + 3\right)^2}$
整理得 $
\left({k^2} + 1\right)\left(3{k^2} - 4\right)= 0$，
而 $k^{2}+1>0$，所以 $3k^{2}-4=0$，
解得 $k = \pm \dfrac{2\sqrt 3 }{3}$，
因为 $k<0$，所以 $k=-\dfrac{2\sqrt 3 }{3}$，
所以点 $P\left(-3\sqrt 3 - 1,6\right)$，点 $M\left(-\sqrt 3 - 1,2\right)$，点 $N\left(-2\sqrt 3 - 1, 1\right)$，
所以 $PM=DN=2\sqrt{7}$，
所以四边形 $DMPN$ 为菱形，
所以以 $DP$ 为对角线的四边形 $DMPN$ 能成为菱形，此时点 $N$ 的坐标为 $\left(-2\sqrt 3-1, 1\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
