如图，锐角 $\triangle ABC$ 内接于圆 $O$，过圆心 $O$ 且垂直于半径 $OA$ 的直线分别交边 $AB,AC$ 于点 $E,F$．设圆 $O$ 在 $B,C$ 两点处的切线相交于点 $P$，求证：直线 $AP$ 平分线段 $EF$．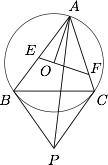
【难度】
【出处】
2012年全国高中数学联赛陕西省预赛（二试）
【标注】
【答案】
略
【解析】
如图，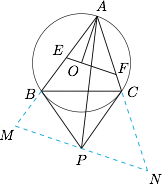
过点 $P$ 作 $EF$ 的平行线，分别交 $AB,AC$ 延长线于点 $M,N$，则$$\angle PMB=\angle AEO=90^\circ-\angle OAE.$$因为 $O$ 是 $\triangle ABC$ 的外心，所以$$\angle OAE=\dfrac12(180^\circ-\angle AOB)=90^\circ-\angle ACB,$$所以$$\angle PMB=\angle ACB.$$又 $PB$ 为圆 $O$ 的切线，所以 $\angle PBM=\angle ACB$，于是$$\angle PMB=\angle PBM,$$故 $PM=PB$．
同理 $PN=PC$．
又因为 $PB=PC$，所以$$PM=PN,$$即 $AP$ 平分线段 $MN$．
因为 $EF\parallel MN$，故直线 $AP$ 平分线段 $EF$．
过点 $P$ 作 $EF$ 的平行线，分别交 $AB,AC$ 延长线于点 $M,N$，则$$\angle PMB=\angle AEO=90^\circ-\angle OAE.$$因为 $O$ 是 $\triangle ABC$ 的外心，所以$$\angle OAE=\dfrac12(180^\circ-\angle AOB)=90^\circ-\angle ACB,$$所以$$\angle PMB=\angle ACB.$$又 $PB$ 为圆 $O$ 的切线，所以 $\angle PBM=\angle ACB$，于是$$\angle PMB=\angle PBM,$$故 $PM=PB$．同理 $PN=PC$．
又因为 $PB=PC$，所以$$PM=PN,$$即 $AP$ 平分线段 $MN$．
因为 $EF\parallel MN$，故直线 $AP$ 平分线段 $EF$．
答案
解析
备注
