如图，四边形 $ABCD$ 的两条对角线相交于点 $O$，$\angle DCO$ 的平分线 $CQ$ 交线段 $OD$ 于 $Q$，连接 $AQ$，作 $OM \perp BC$ 于 $M$，$ON \perp AQ$ 于 $N$，且 $P$ 为 $AB$ 边的中点，$OA=\dfrac {OB \cdot OD}{OC+CD}$．求证：$ PM=PN$．
【难度】
【出处】
2010年全国高中数学联赛吉林省预赛
【标注】
【答案】
略
【解析】
因为 $CQ$ 平分 $\angle DCO$，所以$$\dfrac {DQ}{OQ}=\dfrac {DC}{CO},$$即$$CO=\dfrac {QO}{DQ}\cdot DC.\quad \cdots\cdots \text{ ① }$$又因为 $OA=\dfrac {OB \cdot OD}{OC+CD}$，所以$$OA \cdot (OC+CD)=OB \cdot OD.\quad \cdots\cdots \text{ ② } $$将 ① 代入 ②，得$$OA \cdot \dfrac {DO}{DQ}\cdot CD=OB \cdot OD,$$所以$$OA \cdot \dfrac {1}{DQ}\cdot CD=OB ,$$即 $OA \cdot \dfrac {CO}{OQ} =OB $，故$$OA \cdot OC=OQ \cdot OB,$$所以 $A$，$Q$，$C$，$B$ 四点共圆，从而$$\angle QAO =\angle CBO.$$．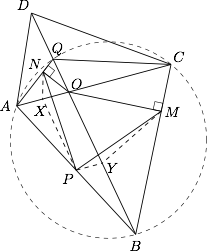
分别取 $OA$，$OB$ 的中点 $X$，$Y$，连结 $NX$，$PX$，$MY$，$PY$，则 $OXPY$ 为平行四边形，所以$$NX=\dfrac 12AO=XO=PY,$$因此\[\begin{split}\angle PXN&=\angle NXO+\angle OXP\\&=2\angle QAO+\angle OXP\\&=2\angle CBO+\angle OYP\\&=\angle MYO+\angle OYP=\angle MYP,\end{split}\]故$$PX=YO=\dfrac 12OB=MY,$$可知 $\triangle PXN \cong \triangle MYP$，因此 $PM=PN$．
分别取 $OA$，$OB$ 的中点 $X$，$Y$，连结 $NX$，$PX$，$MY$，$PY$，则 $OXPY$ 为平行四边形，所以$$NX=\dfrac 12AO=XO=PY,$$因此\[\begin{split}\angle PXN&=\angle NXO+\angle OXP\\&=2\angle QAO+\angle OXP\\&=2\angle CBO+\angle OYP\\&=\angle MYO+\angle OYP=\angle MYP,\end{split}\]故$$PX=YO=\dfrac 12OB=MY,$$可知 $\triangle PXN \cong \triangle MYP$，因此 $PM=PN$．
答案
解析
备注
