如图，在平面直角坐标系 $xOy$ 中，抛物线 $y=-\dfrac 13x^2+2x-\dfrac 53$ 经过 $x$ 轴上点 $A,B$（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$，以点 $A$ 为圆心，作与直线 $BC$ 相切的 $\odot A$ 与 $y$ 轴有怎样的位置关系，并且说明理由．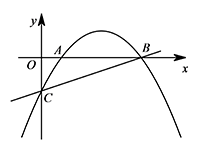
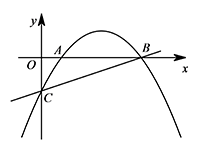
【难度】
【出处】
无
【标注】
【答案】
相交
【解析】
过点 $A$ 作 $AD\perp BC$ 于点 $D$．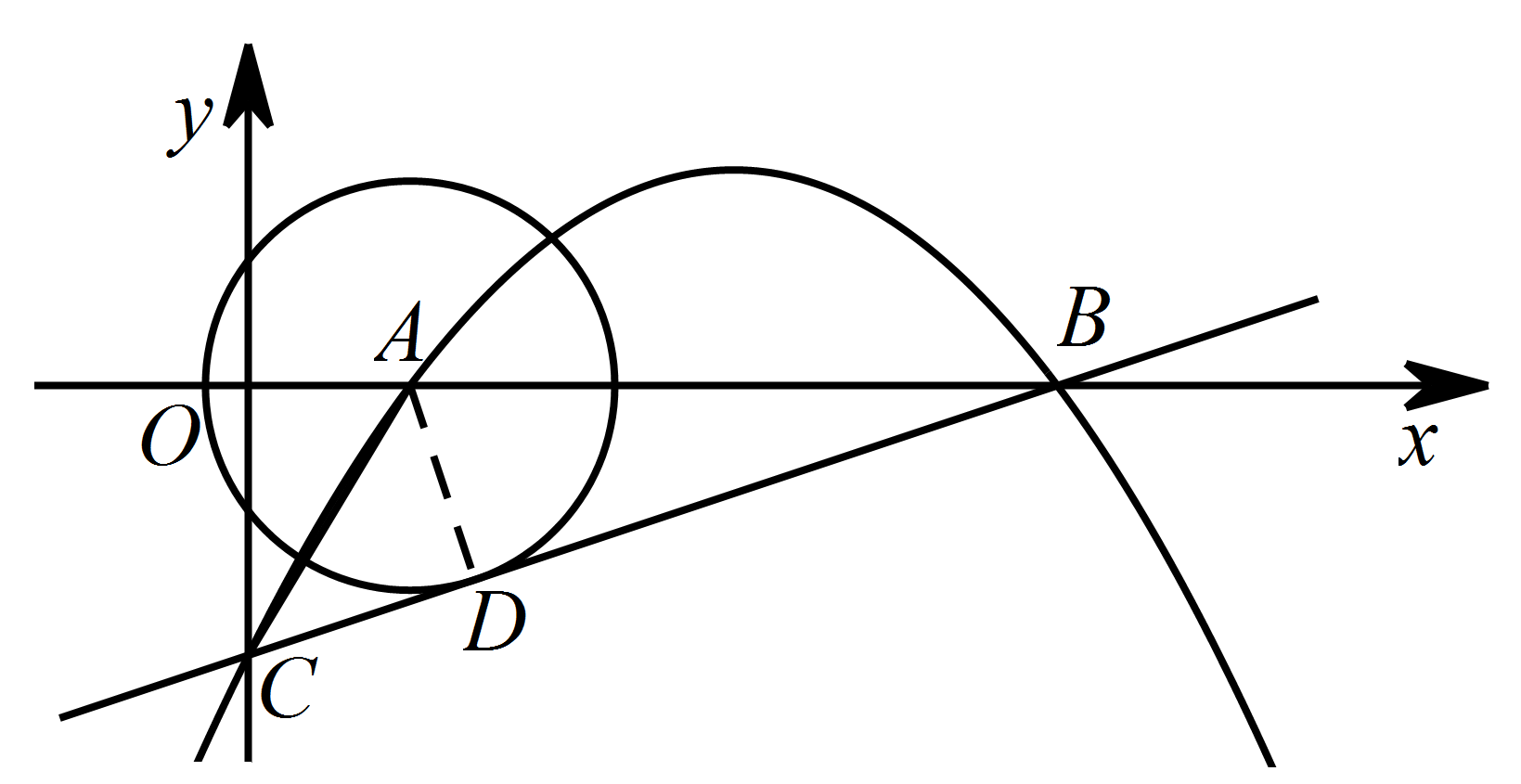
因为 $BC$ 与 $\odot A$ 相切，所以 $AD$ 为 $\odot A$ 的半径．
在 $\mathrm {Rt}\triangle OBC$ 中，
因为 $OC=\dfrac 5 3 $，$OB=5$．
所以 $BC=\sqrt {OC^2+OB^2}=\sqrt {\left(\dfrac 5 3 \right)^2+5^2}=\dfrac 5 3 \sqrt {10}$．
因为 $\triangle BAD\backsim\triangle BCO$，$AB=4$，
所以 $\dfrac {AB} {BC} =\dfrac {AD} {OC} $，
所以 $AD=\dfrac {AB\cdot OC} {BC} =\dfrac {4\times \dfrac 5 3 } {\dfrac {5\sqrt {10}} 3 } =\dfrac 2 5 \sqrt {10}$，
所以 $\odot A$ 的半径为 $\dfrac 2 5 \sqrt {10}$．
因为 $\dfrac 2 5 \sqrt {10}>1$，
所以 $\odot A$ 与 $y$ 轴相交．
因为 $BC$ 与 $\odot A$ 相切，所以 $AD$ 为 $\odot A$ 的半径．在 $\mathrm {Rt}\triangle OBC$ 中，
因为 $OC=\dfrac 5 3 $，$OB=5$．
所以 $BC=\sqrt {OC^2+OB^2}=\sqrt {\left(\dfrac 5 3 \right)^2+5^2}=\dfrac 5 3 \sqrt {10}$．
因为 $\triangle BAD\backsim\triangle BCO$，$AB=4$，
所以 $\dfrac {AB} {BC} =\dfrac {AD} {OC} $，
所以 $AD=\dfrac {AB\cdot OC} {BC} =\dfrac {4\times \dfrac 5 3 } {\dfrac {5\sqrt {10}} 3 } =\dfrac 2 5 \sqrt {10}$，
所以 $\odot A$ 的半径为 $\dfrac 2 5 \sqrt {10}$．
因为 $\dfrac 2 5 \sqrt {10}>1$，
所以 $\odot A$ 与 $y$ 轴相交．
答案
解析
备注
