如图,一次函数 $y=-x+4$ 的图象与 $x,y$ 轴分别相交于点 $A,B$,过点 $A$ 作 $x$ 轴的垂线 $l$,点 $P$ 为直线 $l$ 上的动点,点 $Q$ 为直线 $AB$ 与 $\triangle OAP$ 外接圆的交点,点 $P,Q$ 与点 $A$ 都不重合.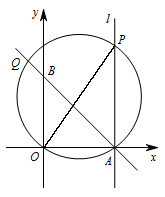

【难度】
【出处】
无
【标注】
-
当点 $P$ 在直线 $l$ 上运动时,是否存在点 $P$ 使得 $\triangle OQB$ 与 $\triangle APQ$ 全等?如果存在,求出点 $P$ 的坐标;如果不存在,请说明理由.标注答案存在,点 $P$ 点坐标为 $\left(4,4\sqrt 2-4\right)$解析因为直线 $y=-x+4$ 与 $x,y$ 轴分别相交于点 $A,B$,
所以点 $A$ 的坐标为 $\left(4,0\right)$,点 $B$ 的坐标为 $\left(0,4\right)$,
所以 $OB=OA=4$,
从而 $AB=\sqrt{OA^2+OB^2}=\sqrt{4^2+4^2}=4\sqrt2$.
如图,若 $\triangle BOQ\cong \triangle AQP$, 所以 $QA=OB=4$,$BQ=PA$,
所以 $QA=OB=4$,$BQ=PA$,
所以 $PA=BQ=AB-AQ=4\sqrt 2-4$.
因为点 $P$ 在第一象限内,且 $P$ 在直线 $x=4$ 上,
所以点 $P$ 点坐标为 $\left(4,4\sqrt 2-4\right)$. -
若点 $M$ 在直线 $l$ 上,且 $\angle POM=90^\circ $,记 $\triangle OAP$ 外接圆和 $\triangle OAM$ 外接圆的面积分别是 ${S_1},{S_2}$,求 $\dfrac{1}{S_1} + \dfrac{1}{S_2}$ 的值.标注答案$\dfrac{1}{S_1}+\dfrac{1}{S_2}=\dfrac{1}{4{\mathrm \pi}}$解析如图,$\triangle OAP$ 外接圆的圆心为 $O_1$,$\triangle OAM$ 外接圆的圆心为 $O_2$,分别过 $O_1,O_2$ 作直线 $l$ 的垂线,垂足为点 $Q,N$.
 令 $PA=a$,$MA=b$,
令 $PA=a$,$MA=b$,
则 $OP^2=OA^2+PA^2=16+a^2$,$OM^2=OA^2+MA^2=16+b^2$.
在 $\mathrm {Rt}\triangle POM$ 中,$PM^2=OP^2+OM^2=a^2+b^2+32$.
因为 $PM^2=\left(PA+AM\right)^2=\left(a+b\right)^2=a^2+2ab+b^2$,
所以 $a^2+b^2+32=a^2+2ab+b^2$,即 $ab=16$.
因为 $PO_1^2=O_1Q^2+QP^2=4+\dfrac14a^2$,$O_2M^2=O_2N^2+MN^2=4+\dfrac14b^2$,
所以 $S_1=\left(\dfrac14a^2+4\right){\mathrm \pi}$,$S_2=\left(\dfrac14b^2+4\right){\mathrm \pi}$.
$\begin{split}\text{从而} \dfrac{1}{S_1}+\dfrac{1}{S_2}&=\dfrac{S_1+S_2}{S_1S_2}\\ &=\dfrac{{\mathrm \pi}\times\left(\dfrac14a^2+4\right)+{\mathrm \pi}\times\left(\dfrac14b^2+4\right)}{{\mathrm \pi}\times\left(\dfrac14a^2+4\right)\times{\mathrm \pi}\times\left(\dfrac14b^2+4\right)}
\\&=\dfrac{4}{\mathrm \pi} \times\dfrac{a^2+b^2+16+16}{16a^2+16b^2+16^2+16^2}
\\&=\dfrac{1}{4{\mathrm \pi}}.\end{split}$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2