查看数据源：5a409d3dfab7080008a76adf
网格纸上小正方形的边长为 $1$，粗线画出的是某几何体的三视图，则该几何体的体积为 \((\qquad)\)
A: $4\pi$
B: $\dfrac{7\pi}2$
C: $\dfrac{7\pi}4$
D: $7\pi$
【难度】
【出处】
2017年清华大学THUSSAT测试理科数学（二测）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的三视图
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
【答案】
C
【解析】
如图，三视图所表示的几何体为横置的圆柱截去 $\dfrac 18$ 后剩余的部分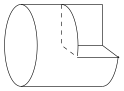．其体积为\[\dfrac 78\cdot \pi\cdot 1^2\cdot 2=\dfrac{7\pi}4.\]
题目 答案 解析 备注
0.112960s