已知抛物线的表达式为 $y=-{x^2}+6x+c$.若 $P,Q$ 是抛物线上位于第一象限的不同两点,$PA,QB$ 都垂直于 $x$ 轴,垂足分别为 $A,B$,且 $\triangle OPA$ 与 $\triangle OQB$ 全等,求证:$c>-\dfrac{21}{4}$.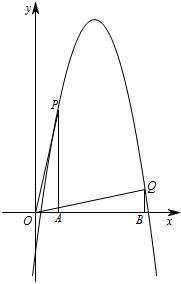

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
因为 $\triangle OAP\cong\triangle QBO$,
所以 $OA=QB$,$PA=OB$.
设点 $P$ 的坐标为 $\left(m,n\right)$,且 $m>0,n>0,m\ne n$,则点 $Q$ 点坐标为 $\left(n,m\right)$,
将这两个点的坐标代入抛物线解析式,得 $\begin{cases}
- {m^2} + 6m+c =n, & ① \\
- n^2+6n+c =m, & ② \end{cases}$
① $-$ ② 得 $n^2-m^2+7\left(m-n\right)=0$,
故有 $n=7-m$.
将其代入方程 ②,得 $ - {m^2} + 7m + \left(c - 7\right) = 0$.
因为存在这样的点,即上述方程有解,
所以其根的判别式 $\Delta={b^2}- 4ac\geqslant 0$,
即 ${7^2}-4\times \left(-1\right)\times \left(c-7\right)\geqslant 0$.
解得 $c\geqslant-\dfrac{21}{4}$.
而当 $c=- \dfrac{21}{4}$ 时,$m=\dfrac{7}{2}$,此时 $n = \dfrac{7}{2}$ 不符合题意.
故 $c>-\dfrac{21}{4}$.
所以 $OA=QB$,$PA=OB$.
设点 $P$ 的坐标为 $\left(m,n\right)$,且 $m>0,n>0,m\ne n$,则点 $Q$ 点坐标为 $\left(n,m\right)$,
将这两个点的坐标代入抛物线解析式,得 $\begin{cases}
- {m^2} + 6m+c =n, & ① \\
- n^2+6n+c =m, & ② \end{cases}$
① $-$ ② 得 $n^2-m^2+7\left(m-n\right)=0$,
故有 $n=7-m$.
将其代入方程 ②,得 $ - {m^2} + 7m + \left(c - 7\right) = 0$.
因为存在这样的点,即上述方程有解,
所以其根的判别式 $\Delta={b^2}- 4ac\geqslant 0$,
即 ${7^2}-4\times \left(-1\right)\times \left(c-7\right)\geqslant 0$.
解得 $c\geqslant-\dfrac{21}{4}$.
而当 $c=- \dfrac{21}{4}$ 时,$m=\dfrac{7}{2}$,此时 $n = \dfrac{7}{2}$ 不符合题意.
故 $c>-\dfrac{21}{4}$.
答案
解析
备注