已知在平面直角坐标系 $xOy$ 中，一次函数 $y=-\dfrac{\sqrt 3}{3}x+1$ 的图象与 $x$ 轴、$y$ 轴分别交于 $A,B$ 两点．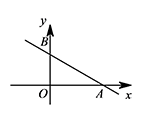
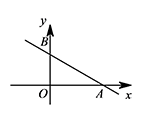
【难度】
【出处】
无
【标注】
-
求 $A,B$ 两点的坐标；标注答案点 $A$ 的坐标为 $\left(\sqrt 3,0\right)$；点 $B$ 的坐标为 $\left(0,1\right)$解析令 $y=0$，即 $-\dfrac{\sqrt 3}{3}x+1=0$，解得 $x=\sqrt 3$，所以点 $A\left(\sqrt 3,0\right)$；
令 $x=0$，得 $y=1$，所以点 $B\left(0,1\right)$． -
如果有一个三角形与 ${\mathrm {Rt}}\triangle AOB$ 全等，且与 ${\mathrm {Rt}}\triangle AOB$ 有一条公共边，请在图中的平面直角坐标内画出满足条件的三角形，这样的三角形有多少个？请分别求出三角形未知的顶点坐标．标注答案这样的三角形共 $9$ 个，未知顶点坐标为 $C_1\left(-\sqrt3,0\right)$，$C_2\left(-\sqrt 3,1\right)$，$C_3\left(\sqrt 3,1\right)$，$C_4\left(\sqrt3,-1\right)$，$C_5\left(0,-1\right)$，$C_6\left(\dfrac{\sqrt 3}{2},\dfrac 32\right)$，$C_7\left(\dfrac{\sqrt 3}{2},-\dfrac 12\right)$，其中以 $C_3$ 为顶点有 $3$ 个不同的三角形解析这样的三角形共 $9$ 个，未知顶点坐标为 $C_1\left(-\sqrt3,0\right)$，$C_2\left(-\sqrt 3,1\right)$，$C_3\left(\sqrt 3,1\right)$，$C_4\left(\sqrt3,-1\right)$，$C_5\left(0,-1\right)$，$C_6\left(\dfrac{\sqrt 3}{2},\dfrac 32\right)$，$C_7\left(\dfrac{\sqrt 3}{2},-\dfrac 12\right)$，其中以 $C_3$ 为顶点有 $3$ 个不同的三角形，如图所示．
$C_6,C_7$ 的求法：如图，作 $C_6M\perp x$ 轴于点 $M$．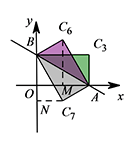
因为 $C_6A=\sqrt 3$，$\angle C_6AM=60^\circ$，
所以 $AM=\dfrac{\sqrt 3}{2}$，$C_6M=\dfrac 32$，
所以 $C_6\left(\dfrac{\sqrt 3}{2},\dfrac 32\right)$．
如图，作 $C_7N\perp y$ 轴于点 $N$，
因为 $BC_7=\sqrt 3$，$\angle BC_7N=60^\circ$，
所以 $NC_7=\dfrac{\sqrt 3}{2}$，$BN=\dfrac 32$，
所以点 $C_7\left(\dfrac{\sqrt 3}{2},-\dfrac 12\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
