在平面直角坐标系 $xOy$ 中，点 $A$ 与点 $B$ 的坐标分别是 $(1,0),(7,0)$，当点 $P$ 在 $y$ 轴正半轴上运动时，$\angle APB$ 是否有最大值？如果有，说明此时 $\angle APB$ 最大的理由，并求出点 $P$ 的坐标，如果没有，也说明理由．
【难度】
【出处】
无
【标注】
【答案】
$P(0,\sqrt 7)$
【解析】
当过点 $A,B$ 的圆与 $y$ 轴正半轴相切于点 $P$ 时，$\angle APB$ 最大，
如果点 $P$ 在 $y$ 轴的正半轴上，设此时圆心为 $E$，则 $E$ 在第一象限，
在 $y$ 轴的正半轴上任取一点 $M$（不与点 $P$ 重合）．
连接 $MA,MB,PA,PB$，设 $MB$ 交于 $\odot E$ 于点 $N$，连接 $NA$，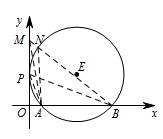
因为点 $P$，点 $N$ 在 $\odot E$ 上，所以 $\angle APB=\angle ANB$．
因为 $\angle ANB$ 是 $\triangle MAN$ 的外角，
所以 $\angle ANB>\angle AMB$，即 $\angle APB>\angle AMB$．
此时，过点 $E$ 作 $EF\perp x$ 轴于 $F$，则 $AF=\dfrac 12AB=3,OF=4$．
连接 $EA,EP$，
因为 $\odot E$ 与 $y$ 轴相切于点 $P$，则 $EP\perp y$ 轴，
所以四边形 $OPEF$ 是矩形，$OP=EF,PE=OF=4$，
所以 $\odot E$ 的半径为 $4$，即 $EA=4$，
所以在 $\rm{Rt}\triangle AEF$ 中，$EF=\sqrt 7$，
所以 $OP=\sqrt 7$，即 $P(0,\sqrt 7)$．
如果点 $P$ 在 $y$ 轴的正半轴上，设此时圆心为 $E$，则 $E$ 在第一象限，
在 $y$ 轴的正半轴上任取一点 $M$（不与点 $P$ 重合）．
连接 $MA,MB,PA,PB$，设 $MB$ 交于 $\odot E$ 于点 $N$，连接 $NA$，
因为点 $P$，点 $N$ 在 $\odot E$ 上，所以 $\angle APB=\angle ANB$．因为 $\angle ANB$ 是 $\triangle MAN$ 的外角，
所以 $\angle ANB>\angle AMB$，即 $\angle APB>\angle AMB$．
此时，过点 $E$ 作 $EF\perp x$ 轴于 $F$，则 $AF=\dfrac 12AB=3,OF=4$．
连接 $EA,EP$，
因为 $\odot E$ 与 $y$ 轴相切于点 $P$，则 $EP\perp y$ 轴，所以四边形 $OPEF$ 是矩形，$OP=EF,PE=OF=4$，
所以 $\odot E$ 的半径为 $4$，即 $EA=4$，
所以在 $\rm{Rt}\triangle AEF$ 中，$EF=\sqrt 7$，
所以 $OP=\sqrt 7$，即 $P(0,\sqrt 7)$．
答案
解析
备注
