我们给出如下定义：两个图形 $\rm{G_1}$ 和 $\rm{G_2}$，在 $\rm{G_1}$ 上的任意一点 $P$ 引出两条垂直的射线与 $\rm{G_2}$ 相交于点 $M,N$，如果 $PM=PN$，我们就称 $M,N$ 为点 $P$ 的垂等点，$PM,PN$ 为点 $P$ 的垂等线段，点 $P$ 为垂等射点．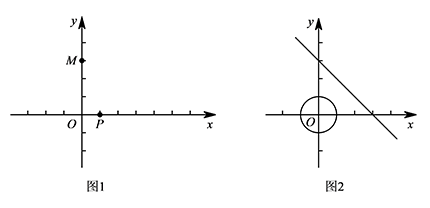
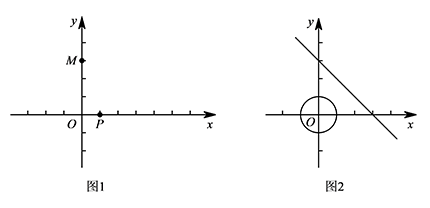
【难度】
【出处】
无
【标注】
-
如果一次函数图象过 $M(0,3)$，点 $M$ 为垂等射点 $P(1,0)$ 的一个垂等点且另一个垂等点 $N$ 也在一次函数图象上，在图1中画出示意图并求出一次函数表达式；标注答案$y=2x+3$ 或 $y=-\dfrac 12x+3$解析① 当点 $N$ 在 $PM$ 的左侧时，如图，作 $NR\perp x$ 轴于点 $R$．
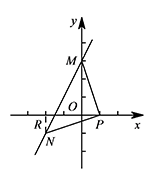易证 $\triangle POM\cong \triangle NRP$，
所以 $NR=PO=1$，$PR=MO=3$，
所以点 $N$ 的坐标为 $(-2,-1)$．
从而直线 $MN$ 的表达式为 $y=2x+3$．
② 当点 $N$ 在 $PM$ 的右侧时，如图，作 $NR\perp x$ 轴于点 $R$．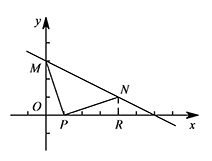
易证 $\triangle POM\cong \triangle NRP$，
所以 $NR=PO=1$，$PR=MO=3$，
所以点 $N$ 的坐标为 $(4,1)$．
从而直线 $MN$ 的表达式为 $y=-\dfrac 12x+3$．
综上所述，该一次函数的表达式为 $y=2x+3$ 或 $y=-\dfrac 12x+3$． -
如图2，以点 $O$ 为圆心，$1$ 为半径作 $\odot O$，垂等射点 $P$ 在 $\odot O$ 上，垂等点在经过 $(3,0),(0,3)$ 的直线上，如果关于点 $P$ 的垂等线段始终存在，求垂等线段 $PM$ 长的取值范围．标注答案$3-\sqrt 2\leqslant PM\leqslant 3-\sqrt 2$解析记经过 $(3,0),(0,3)$ 的直线为 $l$．
如图，过点 $O$ 作 $OQ\perp l$ 于点 $Q$，直线 $OQ$ 交 $\odot O$ 于点 $P_1,P_2$．
过 $P_1$ 作 $x,y$ 轴的垂线，分别交 $l$ 于点 $M_1,N_1$；
过 $P_2$ 作 $x,y$ 轴的垂线，分别交 $l$ 于点 $M_2,N_2$．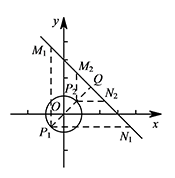
可得 $\angle M_1P_1N_1=90^\circ$，$P_1M_1=P_1N_1$；$\angle M_2P_2N_2=90^\circ$，$P_2M_2=P_2N_2$．
易求 $OQ=\dfrac{3\sqrt 2}{2}$，
所以 $P_1Q=\dfrac{3\sqrt 2}{2}+1$，$P_2Q=\dfrac{3\sqrt 2}{2}-1$，
从而 $P_1M_1=\sqrt 2P_1Q=3+\sqrt 2$，$P_2M_2=\sqrt 2P_2Q=3-\sqrt 2$．
结合图形，可得 $PM$ 的取值范围为 $3-\sqrt 2\leqslant PM\leqslant 3-\sqrt 2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
