在平面直角坐标系 $xOy$ 中，对于半径为 $r(r>0)$ 的 $\odot O$ 和点 $P$，给出如下定义：若 $r\leqslant PO\leqslant \dfrac 32r$，则称点 $P$ 为 $\odot O$ 的“近外点”．
【难度】
【出处】
无
【标注】
-
若点 $P(3,4)$ 是 $\odot O$ 的“近外点”，求 $\odot O$ 的半径 $r$ 的取值范围；标注答案$\dfrac{10}3\leqslant r\leqslant 5$解析由点 $P(3,4)$ 的坐标，可得 $PO=\sqrt{3^2+4^2}=5$．
若点 $P(3,4)$ 是 $\odot O$ 的“近外点”，则有 $r\leqslant PO\leqslant \dfrac 32r$，
解得 $\dfrac{10}3\leqslant r\leqslant 5$． -
当 $\odot O$ 的半径为 $2$ 时，直线 $y=\dfrac{\sqrt 3}3x+b(b\ne 0)$ 与 $x$ 轴交于点 $M$，与 $y$ 轴交于点 $N$，若线段 $MN$ 上存在 $\odot O$ 的“近外点”，求 $b$ 的取值范围．标注答案$b$ 的取值范围为 $-2\sqrt 3\leqslant b\leqslant -\dfrac{2\sqrt 3}{3}$ 或 $\dfrac{2\sqrt 3}{3}\leqslant b\leqslant 2\sqrt 3$解析当 $y=0$，得 $x=-\sqrt 3b$，即点 $M(-\sqrt 3b,0)$；
当 $x=0$，得 $y=b$，即点 $N(0,b)$．
所以 $\tan \angle OMN=\dfrac{ON}{OM}=\dfrac{|b|}{\left|-\sqrt 3b\right|}=\dfrac{\sqrt 3}{3}$，
从而 $\angle OMN=30^\circ$．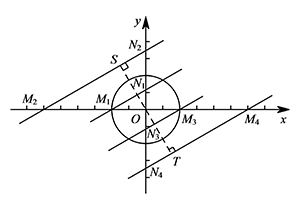
① 若 $b>0$，如图．
1）当点 $M_1$ 的坐标为 $(-2,0)$ 时，则 $b=\dfrac{2\sqrt 3}{3}$；
2）过点 $O$ 作 $OS\perp M_2N_2$ 于点 $S$．
当 $OS=\dfrac 32r=3$ 时，则 $OM_2=2OS=6$，从而 $b=2\sqrt 3$．
结合图形，可得 $\dfrac{2\sqrt 3}{3}\leqslant b\leqslant 2\sqrt 3$．
② 若 $b<0$，如图．同理可得 $-2\sqrt 3\leqslant b\leqslant -\dfrac{2\sqrt 3}{3}$．
综上可得，$b$ 的取值范围为 $-2\sqrt 3\leqslant b\leqslant -\dfrac{2\sqrt 3}{3}$ 或 $\dfrac{2\sqrt 3}{3}\leqslant b\leqslant 2\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
