查看数据源：59364425c2b4e70009388209
在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为梦之点，例如，点 $(1,1),(-2,-2),(\sqrt 2,\sqrt 2),\cdots,$ 都是梦之点，显然梦之点有无数个，已知点 $M(m,3)$，点 $Q$ 是反比例函数 $y=\dfrac 4x$ 图象上异于点 $P(-2,-2)$ 的梦之点，过点 $Q$ 的直线 $l$ 与 $y$ 轴交于点 $A$，$\tan \angle OAQ=1$，若在 $\odot O$ 上存在一点 $N$，使得直线 $MN\parallel l$ 或 $MN\perp l$，求出 $m$ 的取值范围．
【难度】
【出处】
无
【标注】
  • 题型
    >
    代几综合
    >
    函数与圆
【答案】
$-5\leqslant m\leqslant -1$ 或 $1\leqslant m \leqslant 5$
【解析】
因为 $\tan \angle OAQ=1$，所以 $\angle OAQ=45^\circ$．
由已知 $MN\parallel l$ 或 $MN\perp l$，
所以直线 $MN$ 为 $y=-x+b$ 或 $y=x+b$．
当 $MN$ 为 $y=-x+b$ 时，$m=b-3$．
由图可知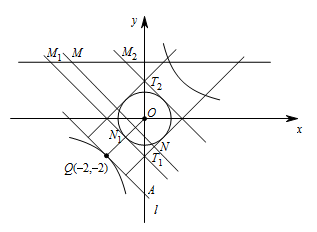，当直线 $MN$ 平移至 $\odot O$ 相切时，
且切点在第四象限时，$b$ 取得最小值，
此时 $MN$ 记为 $M_1N_1$．
其中 $N_1$ 为切点，$T_1$ 为直线与 $y$ 轴的交点．
因为 $\triangle OT_1N_1$ 为等腰直角三角形，
所以 $ON_1=\sqrt 2,OT_1=2$，
所以 $b$ 的最小值是 $-2$，
所以 $m$ 的最小值是 $-5$．
当直线 $MN$ 平移至与 $\odot O$ 相切时，且切点在第二象限时，
$b$ 取得最大值，此时 $MN$ 记为 $M_2N_2$．
其中 $N_2$ 为切点，$T_2$ 为直线 $M_2N_2$ 与 $y$ 轴的交点．
同理可得，$b$ 的最大值为 $2$，$m$ 的最大值为 $-1$．
所以 $m$ 的取值范围为 $-5\leqslant m\leqslant -1$．
当直线 $MN$ 为 $y=x+b$ 时，
同理可得 $m$ 的取值范围为 $1\leqslant m \leqslant 5$．
综上所述，$m$ 的取值范围为 $-5\leqslant m\leqslant -1$ 或 $1\leqslant m \leqslant 5$．
答案 解析 备注
0.118632s