在平面直角坐标系 $xOy$ 中，若点 $P$ 和点 $P_1$ 关于 $y$ 轴对称，点 $P_1$ 和点 $P_2$ 关于直线 $l$ 对称，则称点 $P_2$ 是点 $P$ 关于 $y$ 轴，直线 $l$ 的二次对称点．
【难度】
【出处】
无
【标注】
-
如图，$\odot O$ 的半径为 $1$，若 $\odot O$ 上存在点 $M$，使得点 $M'$ 是点 $M$ 关于 $y$ 轴，直线 $l:x=b$ 的二次对称点，且点 $M'$ 在射线 $y=\dfrac{\sqrt 3}{3}x$（$x\geqslant 0$）上，则 $b$ 的取值范围是
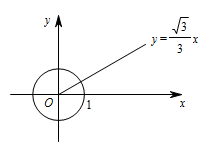标注答案$-\dfrac 12\leqslant b\leqslant 1$解析略 -
$E(t,0)$ 是 $x$ 轴上的动点，$\odot E$ 的半径为 $2$，若 $\odot E$ 上存在点 $N$，使得点 $N'$ 是点 $N$ 关于 $y$ 轴，直线 $l:y=\sqrt 3x+1$ 的二次对称点，且点 $N'$ 在 $y$ 轴上，求 $t$ 的取值范围．
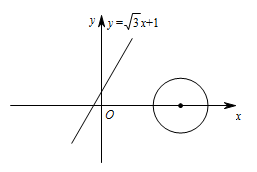标注答案$-4+\sqrt 3\leqslant t\leqslant 4+\sqrt 3$解析将点 $N$ 关于 $y$ 轴的对称点记为点 $P$，
所以点 $P$ 和点 $N'$ 关于直线 $l:y=\sqrt 3x+1$ 对称．
因为直线 $y=\dfrac{\sqrt 3}{3}x+1$ 和 $y$ 轴关于直线 $y=\sqrt 3x+1$ 对称，
所以点 $P$ 在直线 $y=\dfrac{\sqrt 3}{3}x+1$ 上．
因为直线 $y=-\dfrac {\sqrt 3}{3}x+1$ 和直线 $y=\dfrac{\sqrt 3}{3}+1$ 关于 $y$ 轴对称，
所以点 $N$ 在直线 $y=-\dfrac {\sqrt 3}{3}x+1$ 上，
所以符合题意的点 $N$ 是直线 $y=-\dfrac {\sqrt 3}{3}x+1$ 与 $\odot E$ 的公共点．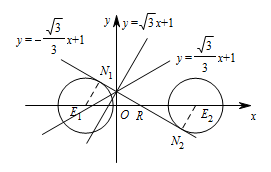
① 当直线 $y=-\dfrac{\sqrt 3}{3}x+1$ 与 $\odot E$ 相离时，则不存在符合题意的点 $N$；
② 当直线 $y=-\dfrac{\sqrt 3}{3}x+1$ 与 $\odot E$ 相切时，如图所示，
则符合题意的点 $N$ 是直线 $y=-\dfrac{\sqrt 3}{3}x+1$ 与 $\odot E$ 相切是的切点，
记直线 $y=-\dfrac{\sqrt 3}{3}x+1 $ 与 $x$ 轴交于点 $R(\sqrt 3,0)$，
若点 $E$ 在点 $R$ 的左侧，
由 $E_1N_1=2$，可得 $RE_1=4,OE_1=4-\sqrt 3$，
所以 $t_1=-4+\sqrt 3$．
若点 $E$ 在点 $R$ 的右侧，
由 $E_2N_2=2$，可得 $RE_2=4,OE_2=4+\sqrt 3$，
所以 $t_2=4+\sqrt 3$；
③ 当直线 $y=-\dfrac{\sqrt 3}{3}x+1$ 与 $\odot E$ 相交时，
$-4+\sqrt 3< t<4+\sqrt 3$，
综上 $t$ 的取值范围是 $-4+\sqrt 3\leqslant t\leqslant 4+\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
