已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 右焦点为 $F$,右准线 $l$ 交 $x$ 轴于点 $N$,过椭圆上一点 $P$ 作 $PM$ 垂直于准线 $l$,垂足为 $M$.若 $PN$ 平分 $\angle FPM$,且四边形 $OFMP$ 为平行四边形,证明 $e>\dfrac23$.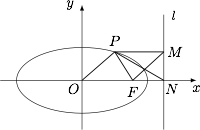

【难度】
【出处】
2012年全国高中数学联赛江苏省复赛(一试)
【标注】
【答案】
略
【解析】
设点 $P(x_0,y_0)$,由对称性,不妨设 $y_0>0$.
四边形 $OFMN$ 为平行四边形,所以$$PM=OF=c,$$于是由$$PM=\dfrac{a^2}{c}-x_0=c,$$得 $x_0=\dfrac{b^2}{c}$.
又点在椭圆上,得$$y_0^2=b^2\left(1-\dfrac{b^4}{a^2c^2}\right).$$当 $PF$ 垂直于 $x$ 轴时,有 $\dfrac{b^2}{c}=c$,得 $e=\dfrac{\sqrt2}{2}$.
当 $PF$ 不垂直于 $x$ 轴时,则有$$k_{PM}=0,k_{PN}=-\dfrac{b\sqrt{1-\frac{b^4}{a^2c^2}}}{c},k_{PF}=\dfrac{b\sqrt{1-\frac{b^4}{a^2c^2}}}{\frac{b^2}{c}-c},$$于是\[\begin{split}&\tan\angle NPM=\left|\dfrac{k_{PM}-k_{PN}}{1+k_{PN}k_{PM}}\right|=\dfrac{b\sqrt{1-\frac{b^4}{a^2c^2}}}{c},\\&\tan\angle NPF=\left|\dfrac{k_{PF}-k_{PN}}{1+k_{PN}k_{PF}}\right|=b\sqrt{1-\dfrac{b^4}{a^2c^2}}\cdot\left|\dfrac{a^2b^2c}{a^2c^4-b^6}\right|,\end{split}\]由 $\tan\angle NPM=\tan\angle NPF$,得$$a^2b^2c^2=a^2c^4-b^6,$$因此$$e^6=(e^2-1)^2,$$即 $e^3+e^2=1$.
因为函数 $f(t)=t^3+t^2$ 在 $t>0$ 时,单调递增,且$$f\left(\dfrac23\right)=\dfrac{8}{27}+\dfrac49=\dfrac{20}{27}<1=f(e),$$所以 $e>\dfrac23$,故结论成立.
四边形 $OFMN$ 为平行四边形,所以$$PM=OF=c,$$于是由$$PM=\dfrac{a^2}{c}-x_0=c,$$得 $x_0=\dfrac{b^2}{c}$.
又点在椭圆上,得$$y_0^2=b^2\left(1-\dfrac{b^4}{a^2c^2}\right).$$当 $PF$ 垂直于 $x$ 轴时,有 $\dfrac{b^2}{c}=c$,得 $e=\dfrac{\sqrt2}{2}$.
当 $PF$ 不垂直于 $x$ 轴时,则有$$k_{PM}=0,k_{PN}=-\dfrac{b\sqrt{1-\frac{b^4}{a^2c^2}}}{c},k_{PF}=\dfrac{b\sqrt{1-\frac{b^4}{a^2c^2}}}{\frac{b^2}{c}-c},$$于是\[\begin{split}&\tan\angle NPM=\left|\dfrac{k_{PM}-k_{PN}}{1+k_{PN}k_{PM}}\right|=\dfrac{b\sqrt{1-\frac{b^4}{a^2c^2}}}{c},\\&\tan\angle NPF=\left|\dfrac{k_{PF}-k_{PN}}{1+k_{PN}k_{PF}}\right|=b\sqrt{1-\dfrac{b^4}{a^2c^2}}\cdot\left|\dfrac{a^2b^2c}{a^2c^4-b^6}\right|,\end{split}\]由 $\tan\angle NPM=\tan\angle NPF$,得$$a^2b^2c^2=a^2c^4-b^6,$$因此$$e^6=(e^2-1)^2,$$即 $e^3+e^2=1$.
因为函数 $f(t)=t^3+t^2$ 在 $t>0$ 时,单调递增,且$$f\left(\dfrac23\right)=\dfrac{8}{27}+\dfrac49=\dfrac{20}{27}<1=f(e),$$所以 $e>\dfrac23$,故结论成立.
答案
解析
备注