设 $A,B$ 是圆 $O_1$ 与圆 $O_2$ 的两个交点,过 $A$ 作直线分别交圆 $O_1$,圆 $O_2$ 于 $C,D$ 两点,过 $C,D$ 两点分别作圆 $O_1$ 与圆 $O_2$ 的切线,并过 $B$ 点分别作这两条切线的垂线,垂足分别为 $P,Q$.求证:$PQ$ 是以 $AB$ 为直径的圆的切线.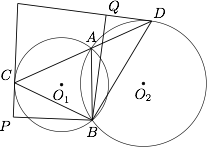

【难度】
【出处】
2012年全国高中数学联赛江苏省复赛(加试)
【标注】
【答案】
略
【解析】
设 $CP,DQ$ 相交于 $E$ 点,则$$\angle BDQ=180^\circ-\angle BAD=\angle BAC=\angle BCP,$$故 $B,C,E,D$ 四点共圆,即点 $B$ 在 $\triangle CDE$ 的外接圆上.
作 $BH\perp CD$ 于 $H$,由 $\mathrm{Simson}$ 定理,得 $P,H,Q$ 三点共线.
因为 $\triangle AHB$ 的外接圆即是以 $AB$ 为直径的圆,设 $O$ 为 $AB$ 的中点,只要证明 $OH\perp PQ$.
事实上,$$\begin{split}\angle OHQ&=\angle OHD+\angle DHQ\\&=\angle OAH+\angle DBQ\\&=\angle BDQ+\angle DBQ\\&=90^\circ.\end{split}$$因此,$OH\perp PQ$.
作 $BH\perp CD$ 于 $H$,由 $\mathrm{Simson}$ 定理,得 $P,H,Q$ 三点共线.
因为 $\triangle AHB$ 的外接圆即是以 $AB$ 为直径的圆,设 $O$ 为 $AB$ 的中点,只要证明 $OH\perp PQ$.
事实上,$$\begin{split}\angle OHQ&=\angle OHD+\angle DHQ\\&=\angle OAH+\angle DBQ\\&=\angle BDQ+\angle DBQ\\&=90^\circ.\end{split}$$因此,$OH\perp PQ$.
答案
解析
备注