如图，在平面直角坐标系中，已知抛物线 $ y=ax^2+bx+c $ 交 $ x $ 轴于 $ A\left(2,0\right) $，$ B\left(6,0\right) $ 两点，交 $ y $ 轴于点 $ C\left(0,2\sqrt 3\right) $．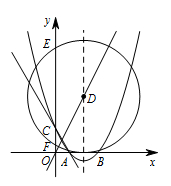
【难度】
【出处】
无
【标注】
-
若此抛物线的对称轴与直线 $ y=2x $ 交于点 $D$，作 $\odot D$ 与 $x$ 轴相切，$\odot D$ 交 $ y $ 轴于点 $E$、$F$ 两点，求劣弧 $EF$ 的长；标注答案$ \dfrac{16}{3}\mathrm \pi $解析因为抛物线 $ y=ax^2+bx+c $ 经过点 $ A\left(2,0\right) $，$ B\left(6,0\right) $，$ C\left(0,2\sqrt 3\right) $，
所以 $\begin{cases}4a+2b+c=0,\\ 36a+6b+c=0,\\ c=2\sqrt 3,\end{cases}$ 解得 $\begin{cases}a=\dfrac{\sqrt 3}{6},\\ b=-\dfrac 43\sqrt 3,\\ c=2\sqrt 3.\end{cases}$
所以抛物线的解析式为 $ y=\dfrac{\sqrt 3}{6}x^2-\dfrac 43\sqrt 3x+2\sqrt 3 $．
易知抛物线的对称轴是，把 $ x=4 $ 代入 $ y=2x $ 得 $ y=8 $，
所以点 $ D $ 的坐标为 $ \left(4,8\right) $．
因为 $\odot D $ 与 $ x $ 轴相切，
所以 $ \odot D $ 的半径为 $ 8 $．
连接 $ DE $、$ DF $，作 $ DM\perp y $ 轴，垂足为点 $ M $．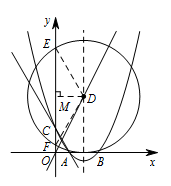
在 $ \mathrm {Rt}\triangle MFD $ 中，$ FD=8 $，$ MD=4 $．
所以 $ \cos \angle MDF= \dfrac 12 $．
所以 $ \angle MDF=60^\circ $，
所以 $ \angle EDF=120^\circ $．
所以劣弧 $ EF $ 的长为 $ \dfrac{120}{180}\times \mathrm \pi\times 8=\dfrac{16}{3}\mathrm \pi $． -
$P$ 为此抛物线在第二象限图象上的一点，$PG$ 垂直于 $ x $ 轴，垂足为点 $G$，试确定 $P$ 点的位置，使得 $\triangle PGA$ 的面积被直线 $AC$ 分为 $ 1:2 $ 两部分．标注答案点 $ P $ 坐标为 $ \left(-3,\dfrac{15}{2}\sqrt 3\right) $ 或 $ \left(-12,42\sqrt 3\right) $ 时，$ \triangle PGA $ 的面积被直线 $ AC $ 分成 $ 1:2 $ 两部分解析
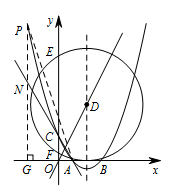设直线 $ AC $ 的解析式为 $ y=kx+b $，
因为直线 $ AC $ 经过点 $ A\left(2,0\right) $，$ C\left(0,2\sqrt 3\right) $．
所以 $\begin{cases}2k+b=0,\\ b=2\sqrt 3 ,\end{cases}$ 解得 $\begin{cases}k=-\sqrt 3,\\ b=2\sqrt 3 .\end{cases}$
所以直线 $ AC $ 的解析式为 $ y=-\sqrt 3x+2\sqrt 3 $．
设点 $ P\left(m,\dfrac{\sqrt 3}{6}m^2-\dfrac 43\sqrt 3m+2\sqrt 3\right)\left(m<0\right) $，$ PG $ 交直线 $ AC $ 于 $ N $，
则点 $ N $ 坐标为 $ \left(m,-\sqrt 3m+2\sqrt 3\right) $．
因为 $S_{\triangle PNA}:S_{\triangle GNA}=PN:GN $．
所以 ① 若 $ PN:GN=1:2 $，则 $ PG:GN=3:2 $，$ PG=\dfrac 32 GN $．
即 $ \dfrac{\sqrt 3}{6}m^2-\dfrac 43\sqrt 3m+2\sqrt 3=\dfrac 32\left(-\sqrt 3m+2\sqrt 3\right) $．
解得 $ m_1=-3 $，$ m_2=2 $（舍去）．
当 $ m=-3 $ 时，$ \dfrac{\sqrt 3}{6}m^2-\dfrac 43\sqrt 3m+2\sqrt 3=\dfrac{15}{2}\sqrt 3 $．
所以此时点 $ P $ 的坐标为 $ \left(-3,\dfrac{15}{2}\sqrt 3\right) $．
② 若 $ PN:GN=2:1 $，则 $ PG:GN=3:1 $，$ PG=3GN $．
即 $ \dfrac{\sqrt 3}{6}m^2-\dfrac 43\sqrt 3m+2\sqrt 3=3\left(-\sqrt 3m+2\sqrt 3\right) $．
解得 $ m_1=-12 $，$ m_2=2 $（舍去）．
当 $ m_1=-12 $ 时，$ \dfrac{\sqrt 3}{6}m^2-\dfrac 43\sqrt 3m+2\sqrt 3=42\sqrt 3 $．
所以此时点 $ P $ 的坐标为 $ \left(-12,42\sqrt 3\right) $．
综上所述，当点 $ P $ 坐标为 $ \left(-3,\dfrac{15}{2}\sqrt 3\right) $ 或 $ \left(-12,42\sqrt 3\right) $ 时，$ \triangle PGA $ 的面积被直线 $ AC $ 分成 $ 1:2 $ 两部分．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
