如图,在平面直角坐标系中,$\odot A$ 与 $ x $ 轴相交于 $C\left(-2,0\right),D\left(-8,0\right)$ 两点,与 $y$ 轴相切于点 $B\left(0,4\right)$.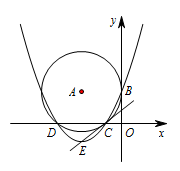

【难度】
【出处】
无
【标注】
-
设经过 $B,C,D$ 三点的抛物线的顶点为 $E$,证明:直线 $CE$ 与 $\odot A$ 相切;标注答案略解析设抛物线的函数表达式为 $y=ax^2+bx+c$,
则 $\begin{cases} 4=c, \\ 0=4a-2b+c, \\ 0=64a-8b+c,\end{cases}$ 解得 $\begin{cases} a=\dfrac 14, \\ b=\dfrac 52, \\ c=4.\end{cases}$
所以经过 $B,C,D$ 三点的抛物线的函数表达式为 $y=\dfrac 14x^2+\dfrac 52x+4$.
因为 $ y=\dfrac 14x^2+\dfrac 52x+4=\dfrac 14\left(x+5\right)^2-\dfrac 94$,
所以 $E\left(-5,-\dfrac 94\right)$.
设直线 $CE$ 的函数表达式为 $y=mx+n$,
则 $\begin{cases} 0=-2m+n, \\ -\dfrac 94=-5m+n,\end{cases}$ 解得 $\begin{cases} m=\dfrac 34, \\ n=\dfrac 32.\end{cases}$
所以直线 $CE$ 的函数表达式为 $y=\dfrac 34x+\dfrac 32$.
当 $x=0$ 时,$y=\dfrac 32$,
故直线 $CE$ 与 $y$ 轴交于点 $G$ 的坐标为 $\left(0,\dfrac 32\right)$.
如图,连接 $AB,AC,AG$.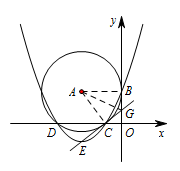 则 $BG=OB-OG=4-\dfrac 32=\dfrac 52$,$CG=\sqrt {OC^2+OG^2}=\sqrt {2^2+\left(\dfrac 32\right)^2}=\dfrac 52$,
则 $BG=OB-OG=4-\dfrac 32=\dfrac 52$,$CG=\sqrt {OC^2+OG^2}=\sqrt {2^2+\left(\dfrac 32\right)^2}=\dfrac 52$,
所以 $BG=CG$,$AB=AC$,$AG=AG$,
所以 $\triangle ABG\cong \triangle ACG$,
所以 $ \angle ACG=\angle ABG$.
因为 $ \odot A$ 与 $y$ 轴相切于点 $B\left(0,4\right)$,
所以 $ \angle ABG=90^\circ$,
所以 $ \angle ACG=\angle ABG=90^\circ$.
因为点 $C$ 在 $\odot A$ 上,
所以直线 $CE$ 与 $\odot A$ 相切. -
在 $x$ 轴下方的抛物线上,是否存在一点 $F$,使 $\triangle BDF$ 面积最大,最大值是多少?并求出点 $F$ 的坐标.标注答案存在点 $F$,使 $\triangle BDF$ 的面积最大.点 $F$ 为 $\left(-4,-2\right)$解析如图,连接 $BD,BF,DF$.
 设点 $F$ 的坐标为 $\left(t,\dfrac 14t^2+\dfrac 52t+4\right)$.
设点 $F$ 的坐标为 $\left(t,\dfrac 14t^2+\dfrac 52t+4\right)$.
过点 $F$ 作 $FH \parallel y$ 轴,交 $BD$ 于点 $H$.
设直线 $BD$ 的函数表达式为 $y=kx+d$,
则 $\begin{cases} 4=d, \\ 0=-8k+d,\end{cases}$ 解得 $\begin{cases} k=\dfrac 12,\\ d=4.\end{cases}$
所以直线 $BD$ 的函数表达式为 $y=\dfrac 12x+4$,
所以 $ FH=\dfrac 12t+4-\left(\dfrac 14t^2+\dfrac 52t+4\right)=-\dfrac 14t^2-2t$,
所以
$\begin{split} S_{\triangle BDF}&=S_{\triangle DHF}+S_{\triangle BHF}\\&=\dfrac 12\cdot DO\cdot FH\\&=\dfrac 12\times 8\times \left(-\dfrac 14t^2-2t\right)\\&=-t^2-8t\\&=-\left(t+4\right)^2+16.\end{split}$
所以当 $t=-4$ 时,$S_{\triangle BDF}$ 最大,最大值为 $16$.
当 $t=-4$ 时,$\dfrac 14t^2+\dfrac 52t+4=\dfrac 14\times \left(-4\right)^2+\dfrac 52\times \left(-4\right)+4=-2$,
此时点 $F$ 为 $\left(-4,-2\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2