如图,已知 $A,B$ 是椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的左右顶点,$P,Q$ 是该椭圆上不同于顶点的两点,且直线 $AP$ 与 $QB$,$PB$ 与 $AQ$ 分别交于点 $M,N$.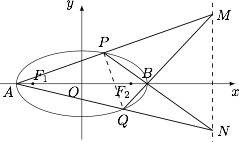

【难度】
【出处】
2012年全国高中数学联赛贵州省预赛
【标注】
-
求证:$MN\perp AB$;标注答案略解析设 $P(a\cos\alpha,b\sin\alpha),Q(a\cos\beta,b\sin\beta)$,由 $A(-a,0),B(a,0)$ 得\[\begin{split}&l_{AP}:a(1+\cos\alpha)y=b\sin\alpha(x+a),\qquad\qquad\cdots\cdots\text{ ① }\\&l_{QB}:a(\cos\beta-1)y=b\sin\beta(x-a),\qquad\qquad\cdots\cdots\text{ ② }\end{split}\]联立 $\text{ ①② }$ 消去 $y$,得$$\sin\alpha(\cos\beta-1)(x+a)=\sin\beta(1+\cos\alpha)(x-a),$$等价于$$[\sin\alpha(\cos\beta-1)-\sin\beta(1+\cos x)]x=a[\sin\alpha(1-\cos\beta)-\sin\beta(1+\cos\alpha)],$$即$$[\sin(\alpha-\beta)-\sin\alpha-\sin\beta]x=a[\sin\alpha-\sin\beta-\sin(\beta+\alpha)],$$所以$$\cos\dfrac{\alpha-\beta}{2}\left(\sin\dfrac{\alpha-\beta}{2}-\sin\dfrac{\alpha+\beta}{2}\right)x=a\cos\dfrac{\alpha+\beta}{2}\left(\sin\dfrac{\alpha-\beta}{2}-\sin\dfrac{\alpha+\beta}{2}\right),$$因为 $P,Q$ 不同于顶点,上式等价于$$x_M=\dfrac{a\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}},$$同理,$x_N=\dfrac{a\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}}$,故 $x_M=x_N$,所以 $MN\perp AB$.
-
若弦 $PQ$ 过椭圆的右焦点 $F_2$,求直线 $MN$ 的方程.标注答案$x=\dfrac{a^2}{c}$解析注意到 $\overrightarrow{F_2P}=(a\cos\alpha-c,b\sin\alpha)$,$\overrightarrow{F_2Q}=(a\cos\alpha-c,b\sin\beta)$,由 $P,F_2,Q$ 三点共线,得 $\overrightarrow{F_2P}$ 与 $\overrightarrow{F_2Q}$ 共线,因此$$\sin\beta(a\cos\alpha-c)=\sin\alpha(a\cos\beta-c),$$整理得$$a\sin(\alpha-\beta)=c(\sin\alpha-\sin\beta),$$利用和差化积公式,得$$a\sin\dfrac{\alpha-\beta}{2}\cdot\cos\dfrac{\alpha-\beta}{2}=c\cos\dfrac{\alpha+\beta}{2}\cdot\sin\dfrac{\alpha-\beta}{2},$$即$$a\cos\dfrac{\alpha-\beta}{2}=c\cos\dfrac{\alpha+\beta}{2},$$因此$$x_M=x_N=\dfrac{a\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}}=\dfrac{a^2}{c},$$故直线 $MN$ 的方程为 $x=\dfrac{a^2}{c}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2