已知抛物线 $y=ax^2+bx+c$ 的对称轴为直线 $x=2$，且与 $x$ 轴交于 $A,B$ 两点，与 $y$ 轴交于点 $C$．其中 $A\left(1,0\right)$，$C\left(0,-3\right)$．
【难度】
【出处】
无
【标注】
-
求抛物线的解析式；标注答案$y=-x^2+4x-3$解析由题意得 $\begin{cases}a+b+c=0,\\c=-3,\\-\dfrac{b}{2a}=2.\end{cases}$ 解得 $\begin{cases}a=-1,\\b=4,\\c=-3.\end{cases}$
所以抛物线的解析式为 $y=-x^2+4x-3$． -
若点 $P$ 在抛物线上运动（点 $P$ 不与点 $A$ 重合），如图，当 $\triangle PBC$ 面积与 $\triangle ABC$ 的面积相等时，求 $P$ 点的坐标．标注答案点 $P$ 的坐标为：$P_1\left(2,1\right)$，$P_2\left(\dfrac{3-\sqrt{17}}{2},\dfrac{-7-\sqrt{17}}{2}\right)$，$P_3\left(\dfrac{3+\sqrt {17}}{2},\dfrac{-7+\sqrt{17}}{2}\right)$解析令 $-x^2+4x-3=0$，解得 $x_1=1$，$x_2=3$．所以 $B\left(3,0\right)$．
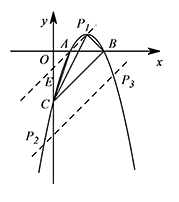① 如图，当点 $P$ 在 $BC$ 上方时，过点 $A$ 作直线 $BC$ 的平行线交抛物线于点 $P_1$，
因为直线 $BC$ 的解析式为 $y=x-3$，
所以设直线 $AP_1$ 的解析式为 $y=x+n$，
因为直线 $AP_1$ 过点 $A\left(1,0\right)$，代入求得 $n=-1$．
所以直线 $AP_1$ 的解析式为 $y=x-1$．
解方程组 $\begin{cases}y=x-1,\\y=-x^2+4x-3.\end{cases}$
得 $\begin{cases}x_1=1,\\y_1=0.\end{cases}\begin{cases}x_2=2,\\y_2=1.\end{cases}$
所以点 $\left(1,0\right)$ 与 $A$ 点重合，所以 $P_1\left(2,1\right)$．
② 当点 $P$ 在 $BC$ 下方时，设直线 $AP_1$ 交 $y$ 轴于点 $E\left(0,-1\right)$，
因为 $EC=2$，把直线 $BC$ 向下平移 $2$ 个单位得到直线 $y=x-5$，交抛物线于点 $P_2,P_3$，
解方程组 $\begin{cases}y=x-5,\\y=-x^2+4x-3.\end{cases}$
得 $\begin{cases}x_1=\dfrac {3+\sqrt {17}}{2},\\y_1=\dfrac {-7+\sqrt {17}}{2}\end{cases}\begin{cases}x_2=\dfrac {3-\sqrt{17}}{2},\\y_2=\dfrac {-7-\sqrt {17}}{2}.\end{cases}$
所以 $P_2\left(\dfrac{3-\sqrt{17}}{2},\dfrac{-7-\sqrt{17}}{2}\right)$，$P_3\left(\dfrac{3+\sqrt {17}}{2},\dfrac{-7+\sqrt{17}}{2}\right)$．
综上所述，点 $P$ 的坐标为：$P_1\left(2,1\right)$，$P_2\left(\dfrac{3-\sqrt{17}}{2},\dfrac{-7-\sqrt{17}}{2}\right)$，$P_3\left(\dfrac{3+\sqrt {17}}{2},\dfrac{-7+\sqrt{17}}{2}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
