如图,已知直线 $y=x+3$ 与 $x$ 轴交于点 $A$,与 $y$ 轴交于点 $B$,将直线在 $x$ 轴下方的部分沿 $x$ 轴翻折,得到一个新函数的图象(图中的“$V$ 形折线”).双曲线 $y=\dfrac kx$ 与新函数的图象交于点 $C\left(1,a\right)$,点 $D$ 是线段 $AC$ 上一动点(不包括端点),过点 $D$ 作 $x$ 轴的平行线,与新函数图象交于另一点 $E$,与双曲线交于点 $P$.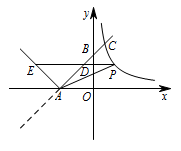

【难度】
【出处】
无
【标注】
-
试求 $\triangle PAD$ 的面积的最大值;标注答案$\triangle PAD$ 的面积的最大值为 $\dfrac{25}{8}$解析直线 $y=x+3$ 关于 $x$ 对称的直线解析式为 $y=-x-3$.
而直线 $y=x+3$ 与 $x$ 轴的交点 $A$ 的坐标为 $\left(-3,0\right)$.
故新函数的解析式为 $y=\begin{cases}x+3\left(x\geqslant -3\right),\\ -x-3\left(x<-3\right).\end{cases}$
因为点 $C(1,a)$ 在新函数图象上,
所以当 $x=1$ 时,$y=1+3=4$,
即点 $C$ 的坐标为 $(1,4)$.
而点 $C\left(1,4\right)$ 在双曲线 $y=\dfrac kx$ 上,
所以 $k=1\times 4=4$,
即双曲线的解析式为 $y=\dfrac 4x$.
由题意可设 点 $D$ 的坐标为 $\left(m,m+3\right)$,且 $-3<m<1$.
则点 $P$ 坐标为 $\left( \dfrac{4}{m+3},m+3\right)$,
所以 $PD=\dfrac{4}{m+3}-m$,
即 $\triangle PAD$ 的面积为
$\begin{split}S&=\dfrac 12\left(\dfrac{4}{m+3}-m\right)\times \left(m+3\right)\\&=-\dfrac 12 m^2-\dfrac 32 m+2\\&=-\dfrac 12\left(m+ \dfrac 32\right)^2+\dfrac{25}{8}.\end{split}$
而 $-3<-\dfrac 32<1$,
所以当 $m=-\dfrac 32$ 时,$S$ 有最大值为 $\dfrac{25}{8}$.
即 $\triangle PAD$ 的面积的最大值为 $\dfrac{25}{8}$. -
探索:在点 $D$ 运动的过程中,四边形 $PAEC$ 能否为平行四边形?若能,求出此时点 $D$ 的坐标;若不能,请说明理由.标注答案在点 $D$ 运动的过程中,四边形 $PAEC$ 不能为平行四边形解析当点 $D$ 为 $AC$ 的中点时,其坐标为 $\left(-1,2\right)$,
此时 $P$ 点的坐标为 $\left(2,2\right)$,$E$ 点的坐标.为 $\left(-5,2\right)$,
所以 $DP=3$,$DE=4$,
因为 $EP$ 与 $AC$ 不能互相平分,
所以四边形 $PAEC$ 不能为平行四边形.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2