如图，在平面直角坐标系中，点 $A\left(10,0\right)$，以 $OA$ 为直径在第一象限内作半圆，$B$ 为半圆上一点，连接 $AB$ 并延长至 $C$，使 $BC=AB$，过 $C$ 作 $CD\perp x$ 轴于点 $D$，交线段 $OB$ 于点 $E$，已知 $CD=8$，抛物线经过 $O,E,A$ 三点．若 $P$ 为抛物线上位于第一象限内的一个动点，以 $P,O,A,E$ 为顶点的四边形面积记作 $S$，则 $S$ 取何值时，相应的点 $P$ 有且只有 $3$ 个？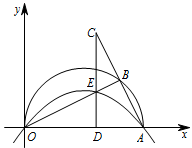
【难度】
【出处】
无
【标注】
【答案】
以 $P,O,A,E$ 为顶点的四边形面积 $S$ 等于 $16$ 时，相应的点 $P$ 有且只有 $3$ 个
【解析】
如图，连接 $OC$．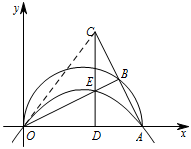
显然 $OB \perp AC$，而 $AB=BC$，
所以直线 $OB$ 是 $AC$ 的垂直平分线，
从而 $OC=OA=10$，
所以在 $\mathrm {Rt}\triangle OCD$ 中，$OD=\sqrt{OC^2-CD^2}=6$，
所以点 $C\left(6,8\right)$．
而点 $A(10,0)$，所以的得到点 $B\left(8,4\right)$，
所以 $OB$ 所在直线的函数关系为 $y=\dfrac 12x$．
又点 $E$ 的横坐标为 $6$，所以点 $E$ 纵坐标为 $3$，即点 $E\left(6,3\right)$．
可设此抛物线的函数关系式为 $y=ax\left(x-10\right)$，
把 $E$ 点坐标代入得 $3=6a\left(6-10\right)$，
解得 $a=-\dfrac 18$．
所以抛物线的函数关系式为 $y=-\dfrac 18x\left(x-10\right)=-\dfrac 18x^2+\dfrac 54x$．
设点 $P\left(p,-\dfrac 18p^2+\dfrac 54p\right)$．
① 如图，若点 $P$ 在 $CD$ 的左侧，连接 $DP$．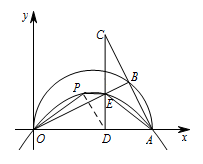
$\begin{split}S_{四边形POAE}&=S_{\triangle POD} +S_{\triangle PDE}+S_{\triangle ADE}\\
&=\dfrac 12 OD\cdot y_P+\dfrac 12 DE\cdot(OD-x_P)+\dfrac 12 AD\cdot ED\\
&=-\dfrac 38p^2+\dfrac{15}4p+\dfrac 32(6-p)+6\\
&=-\dfrac 38p^2+\dfrac 94p+15\\
&=-\dfrac 38(p-3)^2+18\dfrac 38.\end{split}$
② 如图，若点 $P$ 在 $CD$ 的右侧，连接 $DP$．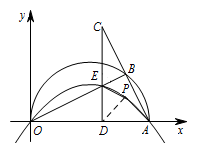
$\begin{split}S_{四边形PAOE}&=S_{\triangle ODE} +S_{\triangle PDE}+S_{\triangle ADP}\\
&=\dfrac 12 OD\cdot DE+\dfrac 12 ED\cdot(x_P-OD)+\dfrac 12 AD\cdot y_P\\
&=9+\dfrac 32(p-6)-\dfrac 14p^2+\dfrac 52p\\&=- \dfrac 14p^2+4p\\
&=-\dfrac 14\left(p-8\right)^2+16.\end{split}$
综上可得，当点 $P$ 在 $CD$ 左侧时，四边形 $POAE$ 的面积最大值为 $18\dfrac 38$；当点 $P$ 在 $CD$ 右侧时，四边形 $PAOE$ 的面积最大值为 $16$．
所以以 $P,O,A,E$ 为顶点的四边形面积 $S$ 等于 $16$ 时，相应的点 $P$ 有且只有 $3$ 个．
显然 $OB \perp AC$，而 $AB=BC$，所以直线 $OB$ 是 $AC$ 的垂直平分线，
从而 $OC=OA=10$，
所以在 $\mathrm {Rt}\triangle OCD$ 中，$OD=\sqrt{OC^2-CD^2}=6$，
所以点 $C\left(6,8\right)$．
而点 $A(10,0)$，所以的得到点 $B\left(8,4\right)$，
所以 $OB$ 所在直线的函数关系为 $y=\dfrac 12x$．
又点 $E$ 的横坐标为 $6$，所以点 $E$ 纵坐标为 $3$，即点 $E\left(6,3\right)$．
可设此抛物线的函数关系式为 $y=ax\left(x-10\right)$，
把 $E$ 点坐标代入得 $3=6a\left(6-10\right)$，
解得 $a=-\dfrac 18$．
所以抛物线的函数关系式为 $y=-\dfrac 18x\left(x-10\right)=-\dfrac 18x^2+\dfrac 54x$．
设点 $P\left(p,-\dfrac 18p^2+\dfrac 54p\right)$．
① 如图，若点 $P$ 在 $CD$ 的左侧，连接 $DP$．
$\begin{split}S_{四边形POAE}&=S_{\triangle POD} +S_{\triangle PDE}+S_{\triangle ADE}\\&=\dfrac 12 OD\cdot y_P+\dfrac 12 DE\cdot(OD-x_P)+\dfrac 12 AD\cdot ED\\
&=-\dfrac 38p^2+\dfrac{15}4p+\dfrac 32(6-p)+6\\
&=-\dfrac 38p^2+\dfrac 94p+15\\
&=-\dfrac 38(p-3)^2+18\dfrac 38.\end{split}$
② 如图，若点 $P$ 在 $CD$ 的右侧，连接 $DP$．
$\begin{split}S_{四边形PAOE}&=S_{\triangle ODE} +S_{\triangle PDE}+S_{\triangle ADP}\\&=\dfrac 12 OD\cdot DE+\dfrac 12 ED\cdot(x_P-OD)+\dfrac 12 AD\cdot y_P\\
&=9+\dfrac 32(p-6)-\dfrac 14p^2+\dfrac 52p\\&=- \dfrac 14p^2+4p\\
&=-\dfrac 14\left(p-8\right)^2+16.\end{split}$
综上可得，当点 $P$ 在 $CD$ 左侧时，四边形 $POAE$ 的面积最大值为 $18\dfrac 38$；当点 $P$ 在 $CD$ 右侧时，四边形 $PAOE$ 的面积最大值为 $16$．
所以以 $P,O,A,E$ 为顶点的四边形面积 $S$ 等于 $16$ 时，相应的点 $P$ 有且只有 $3$ 个．
答案
解析
备注
