如图，一小球从斜坡 $O$ 点处抛出，球的抛出路线可以用二次函数 $y=-x^2+4x$ 刻画，斜坡可以用一次函数 $y=\dfrac 12x$ 刻画．连接抛物线的最高点 $P$ 与点 $O,A$ 得 $\triangle POA$，在 $OA$ 上方的抛物线上存在一点 $M$（$M$ 与 $P$ 不重合），$\triangle MOA$ 的面积等于 $\triangle POA$ 的面积，求点 $M$ 的坐标．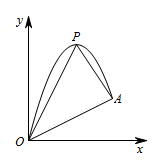
【难度】
【出处】
无
【标注】
【答案】
点 $M$ 的坐标为 $\left(\dfrac 32,\dfrac {15}4\right)$
【解析】
过 $P$ 作 $PM\parallel OA$，交抛物线于点 $ M $，连接 $ OM,AM $，则 $\triangle MOA$ 的面积等于 $\triangle POA$ 的面积．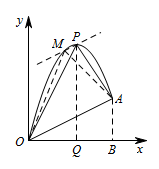
可设直线 $PM$ 的解析式为 $y=\dfrac 12x+b$．
由二次函数解析式可得点 $P$ 的坐标为 $(2,4)$，
将其代入直线 $PM$ 解析式，得 $b=3$，
所以直线 $PM$ 的解析式为 $y=\dfrac 12x+3$．
联立方程组 $\begin{cases}y=\dfrac 12x+3,\\ y=-x^2+4x,\end{cases}$
解得 $\begin{cases}x_1=2,\\y_1=4,\end{cases}\begin{cases}x_2=\dfrac 32,\\ y=\dfrac {15}4.\end{cases}$
所以点 $M$ 的坐标为 $\left(\dfrac 32,\dfrac {15}4\right)$．
可设直线 $PM$ 的解析式为 $y=\dfrac 12x+b$．由二次函数解析式可得点 $P$ 的坐标为 $(2,4)$，
将其代入直线 $PM$ 解析式，得 $b=3$，
所以直线 $PM$ 的解析式为 $y=\dfrac 12x+3$．
联立方程组 $\begin{cases}y=\dfrac 12x+3,\\ y=-x^2+4x,\end{cases}$
解得 $\begin{cases}x_1=2,\\y_1=4,\end{cases}\begin{cases}x_2=\dfrac 32,\\ y=\dfrac {15}4.\end{cases}$
所以点 $M$ 的坐标为 $\left(\dfrac 32,\dfrac {15}4\right)$．
答案
解析
备注
