在直角坐标系 $ xOy $ 中 $ ,A\left(0,2\right) $，$ B\left(-1,0\right) $，将 $ \triangle ABO $ 经过旋转、平移变化后得到如图1所示的 $ \triangle BCD $．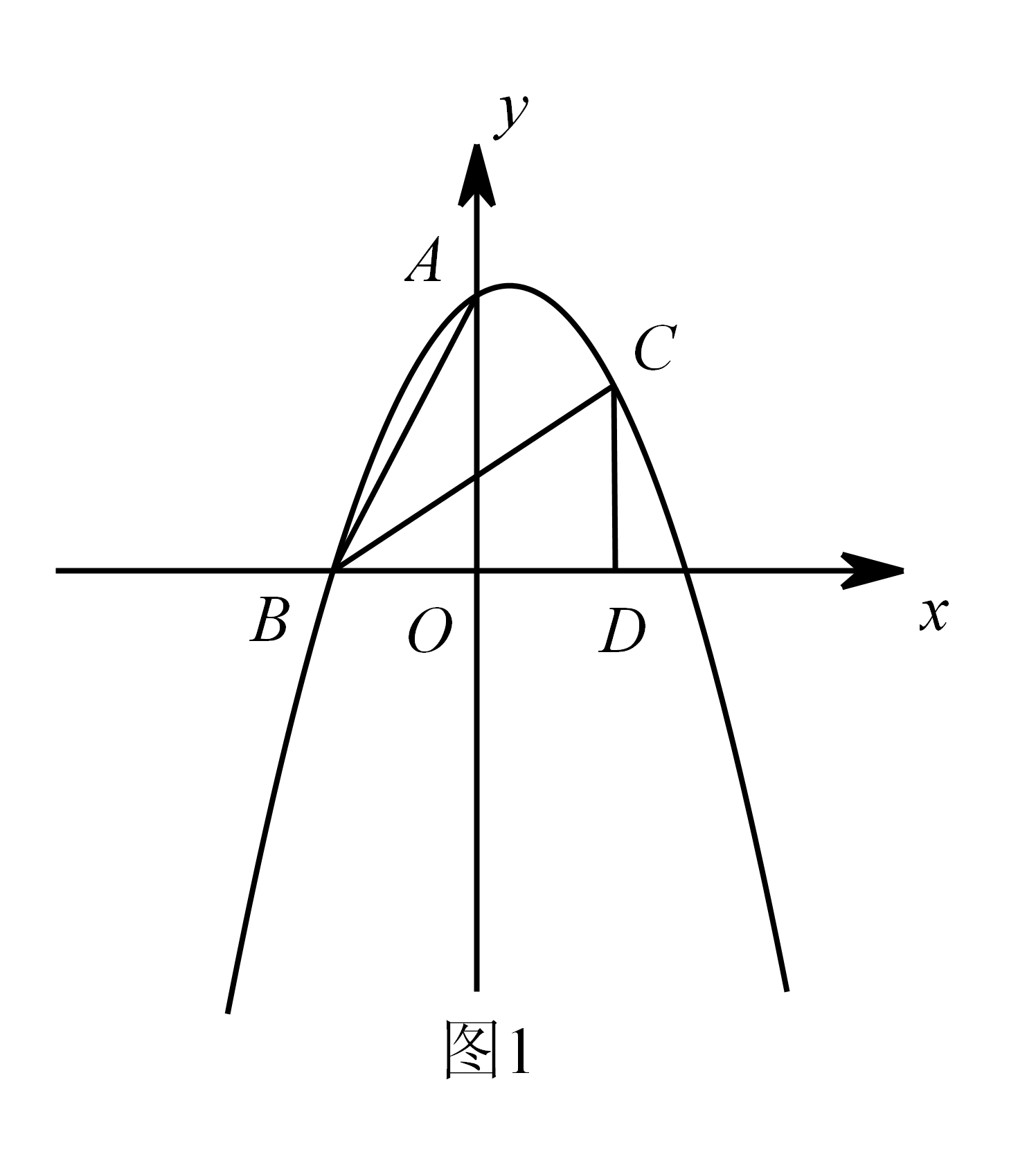
【难度】
【出处】
无
【标注】
-
连接 $ AC $，点 $ P $ 是位于线段 $ BC $ 上方的抛物线上一动点，若直线 $ PC $ 将 $ \triangle ABC $ 的面积分成 $ 1:3 $ 两部分，求此时点 $ P $ 的坐标；标注答案$ P\left(-\dfrac{6}{7} ,\dfrac{23}{49}\right) $解析因为 $ A\left(0,2\right) $，$ B\left(-1,0\right) $，将 $ \triangle ABO $ 经过旋转、平移变化得到 $ \triangle BCD $，
所以 $ BD=OA=2 $，$ CD=OB=1 $，$ \angle BDC=\angle AOB=90^\circ $．
所以 $ C\left(1,1\right) $．
设经过 $ A $，$ B $，$ C $ 三点的抛物线解析式为 $ y=ax^2+bx+c $，
则有 $\begin{cases}a-b+c=0,\\a+b+c=1,\\c=2.\end{cases}$ 解得 $ \begin{cases}a=-\dfrac{3}{2},\\b=\dfrac{1}{2},\\c=2.\end{cases}$
所以抛物线解析式为 $ y=-\dfrac{3}{2} x^2+ \dfrac{1}{2}x+2 $．
如图1所示：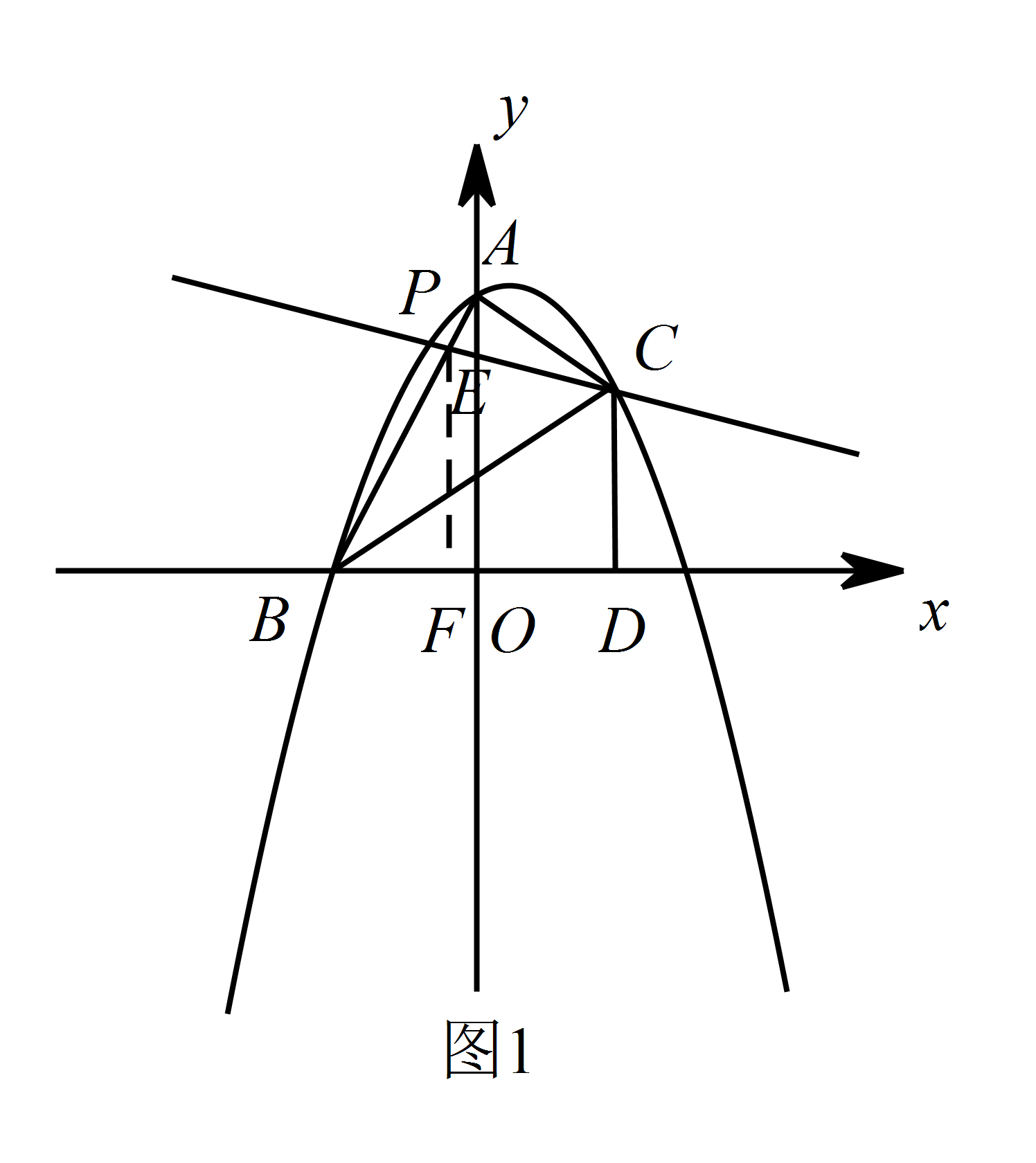
设直线 $ PC $ 与 $ AB $ 交于点 $ E $．
因为直线 $ PC $ 将 $ \triangle ABC $ 的面积分成 $ 1:3 $ 两部分，
所以 $ \dfrac{AE}{BE} = \dfrac{1}{3 } $ 或 $ \dfrac{AE}{BE}=3 $，
过 $ E $ 作 $ EF\perp OB $ 于点 $ F $，则 $ EF\parallel OA $，
所以 $\triangle BEF\backsim \triangle BAO $，
所以 $ \dfrac{EF}{AO}=\dfrac{BE}{BA}=\dfrac{BF}{BO} $．
当 $ \dfrac{AE}{BE} = \dfrac{1}{3 } $ 时，$\dfrac{EF}{2 }=\dfrac{3}{4}=\dfrac{BF}{1}$．
所以 $ EF=\dfrac{3}{2} $，$ BF=\dfrac{3}{4} $，
所以 $E\left(-\dfrac{1}{4} ,\dfrac{3}{2} \right) $．
直线 $ PC $ 解析式为 $ y=-\dfrac{2}{5} x+ \dfrac{7}{5}$，
所以 $ -\dfrac{3}{2} x^2+ \dfrac{1}{2}x+2=-\dfrac{2}{5} x+\dfrac{7}{5 }$，
解得 $ x_1=-\dfrac{2}{5} $，$ x_2=1 $（舍去），
所以 $ P\left(-\dfrac{2}{5} ,\dfrac{39}{25} \right) $．
当 $\dfrac{AE}{BE}=3$ 时，同理可得，$ P\left(-\dfrac{6}{7} ,\dfrac{23}{49}\right) $． -
现将 $ \triangle ABO $，$ \triangle BCD $ 分别向下、向左以 $ 1:2 $ 的速度同时平移，求出在此运动过程中 $ \triangle ABO $ 与 $ \triangle BCD $ 重叠部分面积的最大值．标注答案在此运动过程中 $ \triangle ABO $ 与 $ \triangle BCD $ 重叠部分面积的最大值为 $ \dfrac{25}{52} $解析设 $ \triangle ABO $ 平移的距离为 $ t $，$ \triangle A_1B_1O_1 $ 与 $ \triangle B_2C_1D_1 $ 重叠部分的面积为 $ S $．
由平移得，$ A_1B_1 $ 的解析式为 $ y=2x+2-t $，$ A_1B_1 $ 与 $ x $ 轴交点坐标为 $ \left(\dfrac{t-2}{2} ,0\right) $．
$ C_1B_2 $ 的解析式为 $ y=\dfrac{1}{2} x+t+\dfrac{1}{2} $，$ C_1B_2 $ 与 $ y $ 轴交点坐标为 $ \left(0,t+ \dfrac{1}{2}\right) $．
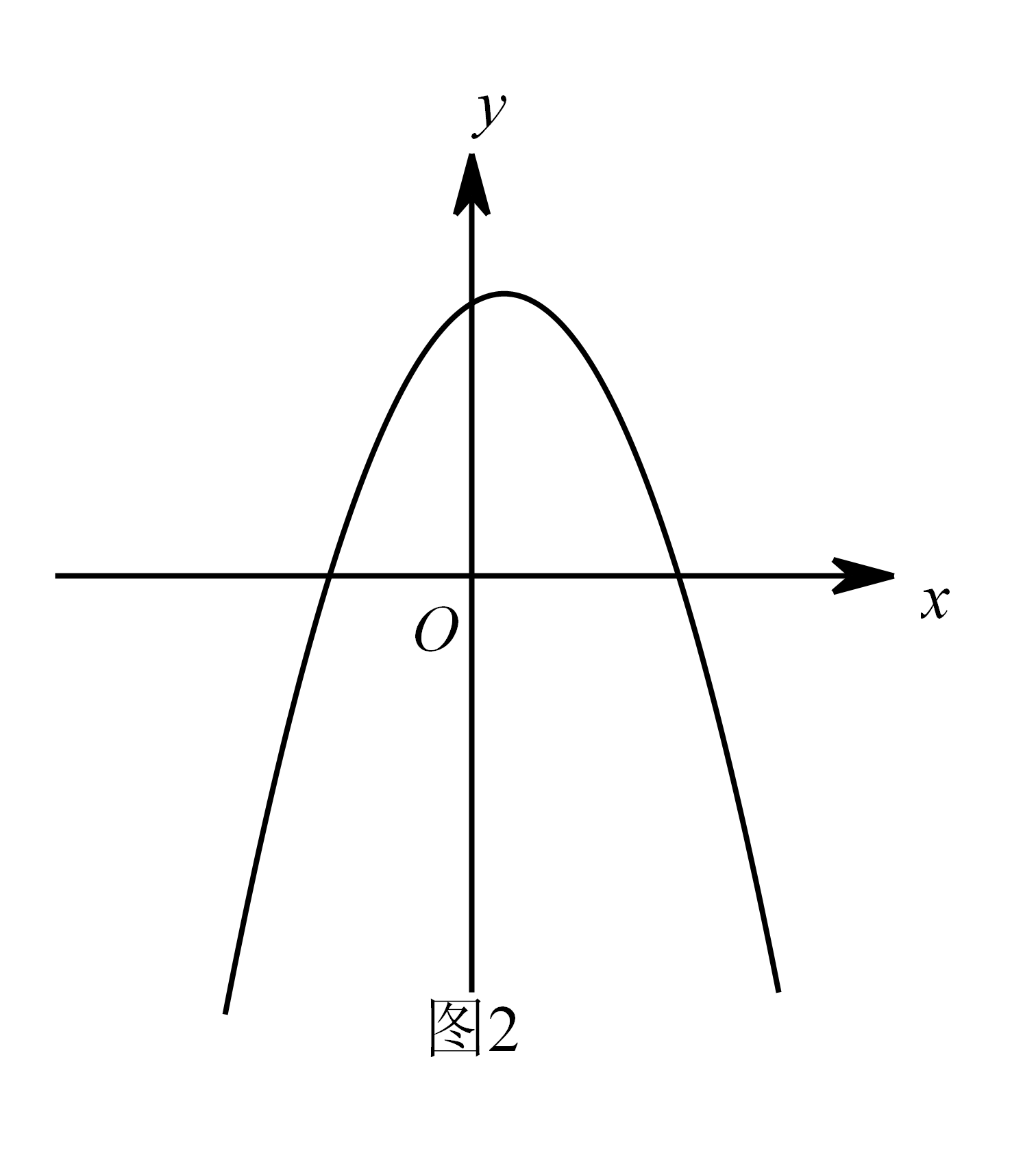
① 如图2所示，
当 $ 0<t<\dfrac{3}{5} $ 时，$ \triangle A_1B_1O_1 $ 与 $ \triangle B_2C_1D_1 $ 重叠部分为四边形．
设 $ A_1B_1 $ 与 $ x $ 轴交于点 $ M $，$ C_1B_2 $ 与 $ y $ 轴交于点 $ N $，$ A_1B_1 $ 与 $ C_1B_2 $ 交于点 $ Q $，连接 $ OQ $．
由 $\begin{cases}y=2x+2-t,\\y=\dfrac{1}{2}x+\dfrac{1}{2 }+t.\end{cases}$ 得 $\begin{cases}x=\dfrac{4t-3}{3},\\y=\dfrac{5t}{3}.\end{cases}$
所以 $ Q\left(\dfrac{4t-3}{3} ,\dfrac{5t}{3} \right) $．
则 $ S=S_{\triangle QMO}+S_{\triangle QON}=\dfrac{1}{2} \times \dfrac{2-t}{2} \times \dfrac{5t}{3} + \dfrac{1}{2}\times \left(t+\dfrac{1}{2}\right)\times \dfrac{3-4t}{3}=-\dfrac{13}{12} t^2+t+\dfrac{1}{4} $，
所以 $ S $ 的最大值为 $\dfrac{25}{52}$．
② 如图3所示，
当 $ \dfrac{3}{5} \leqslant t< \dfrac{4}{5}$ 时，$ \triangle A_1B_1O_1 $ 与 $ \triangle B_2C_1D_1 $ 重叠部分为直角三角形．
设 $ A_1B_1 $ 与 $ x $ 轴交于点 $ H $，$ A_1B_1 $ 与 $ C_1D_1 $ 交于点 $ G $．
所以 $G\left(1-2t,4-5t\right) $，
所以 $D_1H=\dfrac{2-t}{2} +1-2t= \dfrac{4-5t}{2}$，$ D_1G=4-5t $．
所以 $ S= \dfrac{1}{2}D_1H\times D_1G=\dfrac{1}{2} \times \dfrac{4-5t}{2} \times \left(4-5t\right)= \dfrac{1}{4}\left(5t-4\right)^2 $．
所以当 $\dfrac{3}{5} \leqslant t<\dfrac{4}{5} $ 时，$ S $ 的最大值为 $ \dfrac{1}{4}$．
综上所述，在此运动过程中 $ \triangle ABO $ 与 $ \triangle BCD $ 重叠部分面积的最大值为 $ \dfrac{25}{52} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
