如图，已知抛物线 $y=a\left(x+3\right)\left(x-9\right)$ 经过点 $A\left(-3,0\right)$，$B\left(9,0\right)$ 和 $C\left(0,4\right)$．$CD$ 垂直于 $y$ 轴，交抛物线于点 $D$，$DE$ 垂直与 $x$ 轴，垂足为 $E$，$l$ 是抛物线的对称轴，点 $F$ 是抛物线的顶点．若 $\mathrm {Rt}\triangle AOC$ 沿 $x$ 轴向右平移到其直角边 $OC$ 与对称轴 $l$ 重合，再沿对称轴 $l$ 向上平移到点 $C$ 与点 $F$ 重合，得到 $\mathrm {Rt}\triangle A_1O_1F$，求此时 $\mathrm {Rt}\triangle A_1O_1F$ 与矩形 $OCDE$ 重叠部分的图形的面积．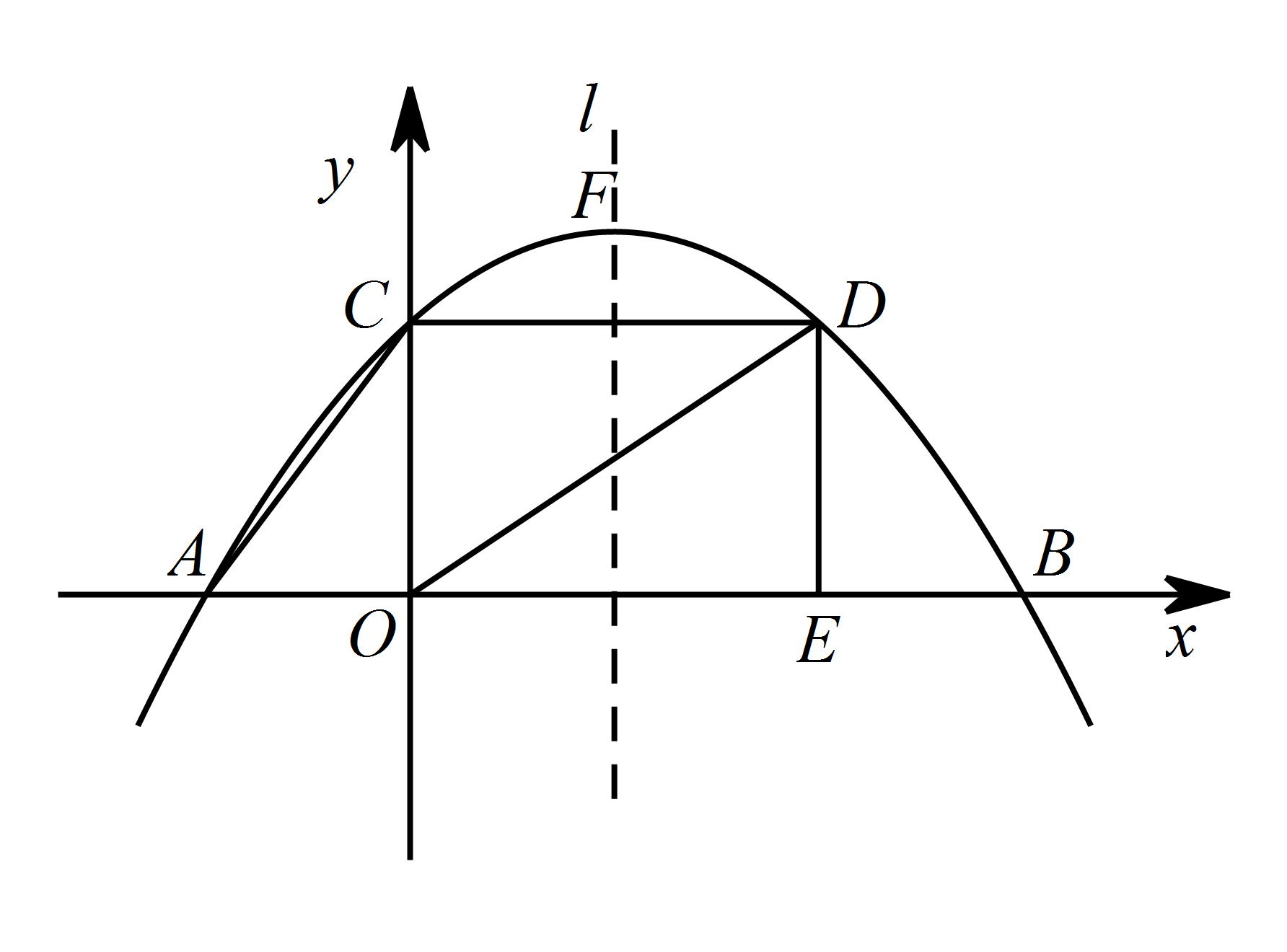
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {16} 3$
【解析】
如图1，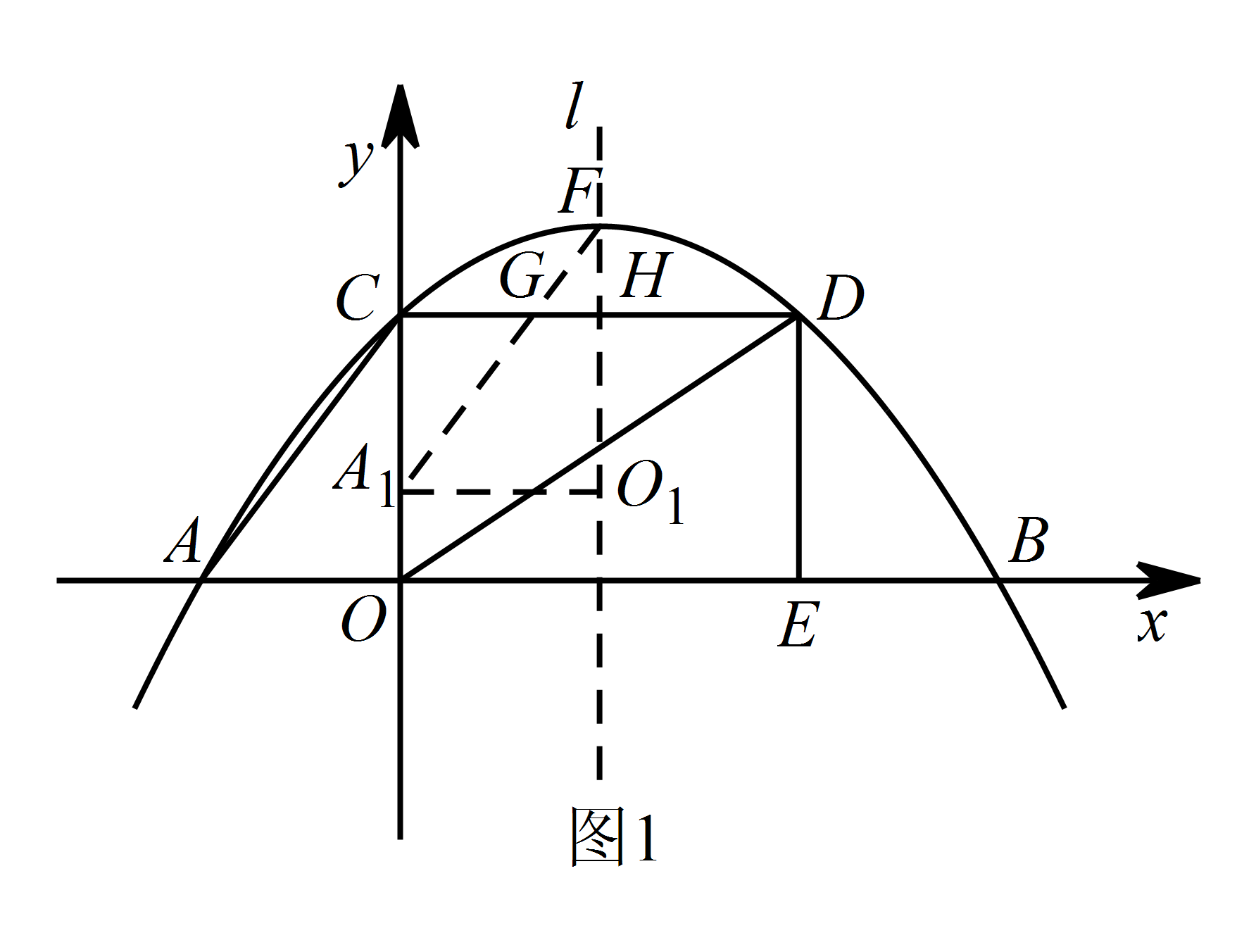
因为点 $F$ 是抛物线 $y=-\dfrac 4 {27} x^2+\dfrac 8 9 x+4$ 的顶点，
所以 $ F\left(3,\dfrac {16} 3 \right)$，
所以 $ FH=\dfrac 4 3 $．
因为 $ GH\parallel A_1O_1$，
所以 $ \dfrac {GH} {A_1O_1} =\dfrac {FH} {FG} $，
所以 $ \dfrac {GH} 3 =\dfrac 3 4 $，
所以 $ GH=1$．
因为 $\mathrm {Rt}\triangle A_1O_1F$ 与矩形 $OCDE$ 重叠部分是梯形 $A_1O_1HG$，
所以
$\begin{split} S_{重叠部分}&=S_{\triangle A_1O_1F}-S_{\triangle FGH}\\&=\dfrac 1 2 A_1O_1\times O_1F-\dfrac 1 2 GH\times FH\\&=\dfrac 1 2 \times 3\times 4-\dfrac 1 2 \times 1\times \dfrac 4 3 \\&=\dfrac {16} 3.\end{split}$
因为点 $F$ 是抛物线 $y=-\dfrac 4 {27} x^2+\dfrac 8 9 x+4$ 的顶点，所以 $ F\left(3,\dfrac {16} 3 \right)$，
所以 $ FH=\dfrac 4 3 $．
因为 $ GH\parallel A_1O_1$，
所以 $ \dfrac {GH} {A_1O_1} =\dfrac {FH} {FG} $，
所以 $ \dfrac {GH} 3 =\dfrac 3 4 $，
所以 $ GH=1$．
因为 $\mathrm {Rt}\triangle A_1O_1F$ 与矩形 $OCDE$ 重叠部分是梯形 $A_1O_1HG$，
所以
$\begin{split} S_{重叠部分}&=S_{\triangle A_1O_1F}-S_{\triangle FGH}\\&=\dfrac 1 2 A_1O_1\times O_1F-\dfrac 1 2 GH\times FH\\&=\dfrac 1 2 \times 3\times 4-\dfrac 1 2 \times 1\times \dfrac 4 3 \\&=\dfrac {16} 3.\end{split}$
答案
解析
备注
