如图,已知抛物线 $y=\dfrac 12x^2-\dfrac 32x-2$ 与 $x$ 轴交于 $A,B$ 两点(点 $A$ 在点 $B$ 的左侧),与 $y$ 轴的负半轴交于点 $C$,点 $P$ 是 $x$ 轴下方抛物线上的一个动点(点 $P$ 与点 $C$ 重合),连接 $PB,PC$.设 $\triangle PBC$ 的面积为 $S$.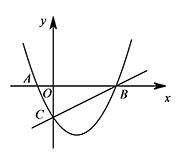
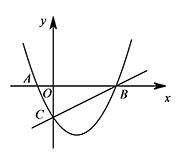
【难度】
【出处】
无
【标注】
-
求 $S$ 的取值范围;标注答案$S$ 的取值范围为 $0<S<5$解析由已知可得 $A\left(-1,0\right)$,$B\left(4,0\right)$,$C\left(0,-2\right)$,
当 $P$ 在 $BC$ 下方时,过点 $P$ 作 $x$ 轴的垂线交 $BC$ 于 $F$.
直线 $BC$ 的解析式为 $y=\dfrac 12x-2.$
设 $P\left(m,\dfrac 12m^2-\dfrac 32m-2\right)$,
那么 $F\left(m,\dfrac 12m-2\right),FP=-\dfrac 12m^2+2m.$ 所以
$\begin{split}S_{\triangle PBC} & =S_{\triangle PBF}+S_{\triangle PCF} \\ &=\dfrac 12FP\left(x_B-x_C\right) \\ & =2FP=-m^2+4m \\ & =-\left(m-2\right)^2+4.\end{split}$
因为 $0<m<4$,
所以当 $P$ 在 $BC$ 下方时,$\triangle PBC$ 的最大值为 $4$.
当 $P$ 在 $BC$ 上方,$x$ 轴下方时,
因为 $S_{\triangle ABC}=5$,所以 $S_{\triangle PBC}<5.$
综上所述,$S$ 的取值范围为 $0<S<5$.
-
若 $\triangle PBC$ 的面积 $S$ 为正整数,则这样的 $\triangle PBC$ 共有 $\underline{\qquad}$ 个.标注答案若 $\triangle PBC$ 的面积 $S$ 为正整数,则这样的 $\triangle PBC$ 共有 $11$ 个.
点 $P$ 在 $x$ 轴下方,$BC$ 上方时,面积为 $1$、$2$、$3$、$4$ 的三角形各 $1$ 个,点 $P$ 在 $BC$ 下方时,面积为 $1$、$2$、$3$ 的三角形各 $2$ 个,面积为 $4$ 的三角形为 $1$ 个解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2