对于集合 $M$，定义函数 $f_M(x)=\begin{cases}-1,&x\in M\\ 1,&x\not\in M\end{cases}$，对于两个集合 $M,N$，定义集合 $M\Delta N=\{x\mid f_M(x)\cdot f_N(x)=-1\}$．已知 $A=\{2,4,6,8,10\}$，$B=\{1,2,4,8,16\}$．
【难度】
【出处】
无
【标注】
-
写出 $f_A(1)$ 和 $f_B(1)$ 的值，并用列举法写出集合 $A\Delta B$；标注答案$f_A(1)=1,f_B(1)=-1$，$A\Delta B=\{1,6,10,16\}$解析$f_A(1)=1,f_B(1)=-1$，$A\Delta B=\{1,6,10,16\}$；
-
用 $\mathrm{card}(M)$ 表示有限集合 $M$ 所含元素的个数，求 $\mathrm{card}(X\Delta A)+\mathrm{card}(X\Delta B)$ 的最小值；标注答案$4$解析如图 $A,B$ 把全集分成四个部分，
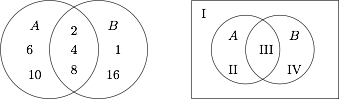设 $X$ 中的元素在第 $I,II,III,IV$ 部分的个数分别为 $x_1,x_2,x_3,x_4$，于是\[\begin{split}\mathrm{card}(X\Delta A)+\mathrm{card}(X\Delta B)&=\mathrm{card}(A)+\mathrm{card}(B)+2\mathrm{card}(X)-2\mathrm{card}(AX)-2\mathrm{card}(BX)\\&=10+2(x_1+x_2+x_3+x_4)-2(x_2+x_3)-2(x_3+x_4)\\&=10+2(x_1-x_3),\end{split}\]而$$x_1\geqslant0,0\leqslant x_3\leqslant \mathrm{card}(AB)=3,$$所以$$\mathrm{card}(X\Delta A)+\mathrm{card}(X\Delta B)\geqslant10+2(0-3)=4,$$此时 $X$ 只需满足 ① $X\subseteq A\Delta B$，② $A\Delta B\subseteq X$． -
有多少个有序集合对 $(P,Q)$，满足 $P,Q\subseteq A\Delta B$，且 $(P\Delta A)\Delta(Q\Delta B)=A\Delta B$？标注答案$16$解析对集合间的运算“$\Delta$”考查其交换律和结合律．
显然“$\Delta$”满足交换律，$A\Delta B=B\Delta A$；
利用韦恩图，不难证明，$(A\Delta B)\Delta C=A\Delta(B\Delta C)$，所以$$(P\Delta A)\Delta(Q\Delta B)=(P\Delta Q)\Delta(A\Delta B),$$一方面，$M\Delta N=N$ 等价于 $M=\varnothing$；另一方面，$M\Delta N=\varnothing$ 等价于 $M=N$，所以 $P=Q$．
由于 $\mathrm{card}(A\Delta B)=4$，因此 $(P,Q)$ 共有 $2^4=16$ 对．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
