已知 $n$ 为正整数,$S_n=\{(a_1,a_2,\cdots,a_{2^n})\mid a_i\in\{0,1\},1\leqslant i\leqslant 2^n\}$,对 $S_n$ 中任意两个元素 $a=(a_1,a_2,\cdots,a_{2^n})$ 和 $b=(b_1,b_2,\cdots,b_{2^n})$,令 $\displaystyle d(a,b)=\sum\limits_{i=1}^{2^n}{|a_i-b_i|}$.若 $A\subseteq S_n$,满足对 $A$ 中任何两个不同的元素 $a$ 和 $b$,都有 $d(a,b)\geqslant 2^{n-1}$,则称 $A$ 为 $S_n$ 的好子集.
【难度】
【出处】
无
【标注】
-
试写出 $S_2$ 的一个好子集 $M$,使 $M$ 中任何两个不同的元素 $a$ 和 $b$,都有 $d(a,b)=2$,且 $M$ 的元素个数为 $4$;标注答案$\{(0000),(0011),(0101),(0110)\}$解析由题意得,$M$ 中的任意两个元素仅有两个位置的数字不同,所以可以写出符合要求的一个集合 $M$ 为 $\{(0000),(0011),(0101),(0110)\}$.
-
试写出 $S_2$ 的一个好子集 $N$,使 $N$ 中任何两个不同的元素 $a$ 和 $b$,都有 $d(a,b)\geqslant2$,且 $N$ 的元素个数为 $8$;标注答案$\{(0000),(0011),(0101),(0110),(1111),(1100),(1010),(1001)\}$解析由题意得,$N$ 中的任意两个元素至少两个位置的数字不同,所以可以写出符合要求的一个集合 $N$ 为 $\{(0000),(0011),(0101),(0110),(1111),(1100),(1010),(1001)\}$.
-
试求 $S_n$ 的好子集 $A$ 的元素个数 $|A|$ 的最大值.标注答案$2^{n+1}$解析约定:
对于 $a=(a_1,a_2,\cdots,a_{2^n})$ 和 $b=(b_1,b_2,\cdots,b_{2^n})$,记$$\overline{a}=(1-a_1,1-a_2,\cdots,1-a_{2^n}),ab=(a_1,a_2,\cdots,a_{2^n},b_1,b_2,\cdots,b_{2^n}),$$对于集合 $A=\{a_1,a_2,\cdots,a_{2^n}\}$,$\displaystyle d(A)=\sum\limits_{i,j=1,i\ne j}^{n}{d(a_i,a_j)}$.
$1^{\circ}$ 首先对于 $S_n$,我们构造满足条件的好子集 $A_n$,且 $A_n=2^{n+1}$.
这里用到归纳构造.
对于 $S_1$,很容易写出 $A_1=\{(0,0),(0,1),(1,0),(1,1)\}$ 符合条件.
现在证明,如果对于 $S_k$,若已经有好子集 $A_k$,且$$|A_k|=2^{k+1},$$那么可以构造好子集 $A_{k+1}$,且$$|A_{k+1}|=2^{k+2}.$$对集合 $A_k$ 中的每个元素 $a$ 改写为 $aa$(记为重型)和 $a\overline{a}$(记为补型),就得到集合 $A_{k+1}$.
接下来证明 $A_{k+1}$ 是好子集.
在 $A_{k+1}$ 中任取两个元素,情形一 若它们为 $A_k$ 中同一元素生成的,那么显然 $d(aa,a\overline{a})=2^k$;情形二 若它们不是 $A_k$ 中同一元素生成的:
如果它们都为重型,设为 $aa,bb$,则$$d(aa,bb)=2d(a,b)\geqslant2^k;$$如果它们都为补型,设为 $a\overline{a},b\overline{b}$,则$$d(a\overline{a},b\overline{b})=d(a,b)+d(\overline{a},\overline{b})=2d(a,b)\geqslant2^k;$$如果它们分别为重型和补型,设为 $aa,b\overline{b}$,则$$d(aa,b\overline{b})=d(a,b)+d(a,\overline{b})=2^k.$$综上,$A_{k+1}$ 是好子集.
$2^{\circ}$ 接下来证明对于 $S_n$,不存在好子集 $A_n$ 且 $|A_n|>2^{n+1}$.
用反证法.
假设对于 $S_n$,存在好子集 $A_n$ 且 $|A_n|>2^{n+1}$,那么$$|A_n|\geqslant2^{n+1}+1,$$于是根据抽屉原理,$A_n$ 中至少存在 $2^n+1$ 个元素,它们的第 $1$ 位都是相同的.
设 $2^n+1$ 个第 $1$ 位相同的元素组成集合 $B$,由于 $B\subseteq A_n$,所以 $B$ 是好子集.
现在用两种方式计算 $d(B)$.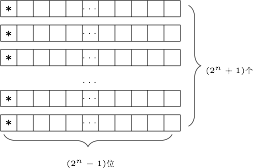
方式一 按 $d(B)$ 的定义,将元素之间的差异进行求和,有$$d(B)\geqslant \mathrm{C}_{2^n+1}^{2}\cdot2^{n-1}=\dfrac{2^{2n}\cdot(2^n+1)}{4},$$方式二 计算所有元素在每一位的差异进行求和.
假设 $B$ 中的所有元素在第 $k$ 位($k\geqslant2$)上有 $x$ 个 $0$,$y$ 个 $1$,那么所有元素在第 $k$ 位上的差异为$$xy\leqslant\left(\dfrac{x+y}{2}\right)^2=\left(\dfrac{2^n+1}{2}\right)^2,$$于是$$d(B)\leqslant (2^n-1)\left(\dfrac{2^n+1}{2}\right)^2=\dfrac{(2^n+1)(2^{2n}-1)}{4}.$$这就推出了矛盾.
因此对于 $S_n$,不存在好子集 $A_n$ 使得 $|A_n|>2^{n+1}$.
综合 $1^\circ$ $2^\circ$,$S_n$ 的好子集 $A$ 的元素个数 $|A|$ 的最大值为 $2^{n+1}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3