我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为"锅线",锅口直径为 $6\mathrm {dm}$,锅盖高 $1\mathrm {dm}$(锅口直径与盖直径视为相同),建立直角坐标系如图所示,如果把锅纵断面的抛物线记为 $C_1$,把锅盖纵断面的抛物线记为 $C_2$.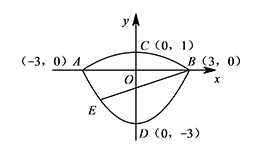
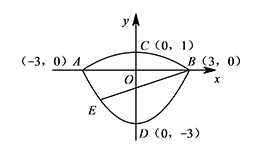
【难度】
【出处】
无
【标注】
-
求 $C_1$ 和 $C_2$ 的解析式;标注答案抛物线 $C_1:y=\dfrac 13x^2-3(-3\leqslant x \leqslant 3)$,
抛物线 $C_2:y=-\dfrac 19x^2+1(-3\leqslant x \leqslant 3)$解析由于抛物线 $C_1$、$C_2$ 都过点 $A\left(-3,0\right)$、$B\left(3,0\right)$,
设抛物线的解析式分别为 $y=a\left(x-3\right)\left(x+3\right),y=b\left(x-3\right)\left(x+3\right)$.
所以 $a=\dfrac 13,b=-\dfrac 19$.
则抛物线 $C_1:y=\dfrac 13x^2-3(-3\leqslant x \leqslant 3)$,
抛物线 $C_2:y=-\dfrac 19x^2+1(-3\leqslant x \leqslant 3)$. -
直线 $BE$:$y=\dfrac 13x-1$,交 $C_1$ 于点 $E$,抛物线 $C_1$ 或 $C_2$ 上是否存在一点 $Q$,使得 $\triangle EBQ$ 的面积最大?若存在,求出 $Q$ 的坐标和 $\triangle EBQ$ 的面积的最大值;若不存在,请说明理由.标注答案存在,$Q$ 点为 $\left(-\dfrac 32,\dfrac 34\right)$.
$\triangle EBQ$ 的最大面积是 $S_{max}=\dfrac{45}{8}$解析存在,点 $Q$ 的坐标为 $\left(-\dfrac 32,\dfrac 34\right)$,最大面积是 $\dfrac{45}{8}$.
【方法一:等积变换法】因为 $E\left(-2,-\dfrac 53\right)$,
如图,作直线 $l\parallel $ 直线 $BE$,设直线 $l$:$y=\dfrac 13x+b$.
① 当直线 $l$ 与抛物线 $C_1$ 只有一个交点时:
$\dfrac 13x+b=\dfrac 13x^2-3$,即 $x^2-x-\left(3b+9\right)=0$.
因为 $\Delta=0$,所以 $b=-\dfrac{37}{12}$,
直线 $Q_1M$:$y=\dfrac 13x-\dfrac{37}{12}$,
所以 $M\left(\dfrac{37}{4},0\right),$ $Q_1\left(\dfrac 12,-\dfrac{35}{12}\right)$.
$S_{\triangle EQ_1B}=S_{\triangle EBM}=\dfrac 12\times BM\times|y_E|=\dfrac{125}{24}$,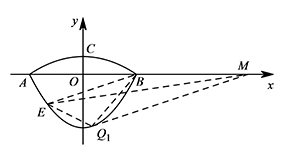 ② 当直线 $l$ 与抛物线 $C_2$ 只有一个交点时:
② 当直线 $l$ 与抛物线 $C_2$ 只有一个交点时:
$\dfrac 13x+b=-\dfrac 19x^2-1$,即 $x^2+3x+9b-9=0$.
因为 $\Delta=0$,所以 $b=\dfrac 54$,
直线 $Q_2N$:$y=\dfrac 13x+\dfrac 54$,
所以 $N\left(-\dfrac{15}{4},0\right),$ $Q_2\left(-\dfrac 32,\dfrac 34\right)$.
$S_{\triangle EQ_2B}=S_{\triangle NBE}=\dfrac 12\times BN\times|y_E|=\dfrac{45}{8}$,
因为 $\dfrac{45}{8}>\dfrac{125}{24}$,
所以符合条件的 $Q$ 点为 $\left(-\dfrac 32,\dfrac 34\right)$.
$\triangle EBQ$ 的最大面积是 $S_{max}=\dfrac{45}{8}$.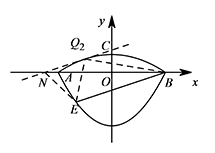 【方法二:割补法】当点 $Q$ 在 $C_1$ 上时,可设 $Q\left(x,\dfrac 13x^2-3\right)$,
【方法二:割补法】当点 $Q$ 在 $C_1$ 上时,可设 $Q\left(x,\dfrac 13x^2-3\right)$,
过 $Q$ 作 $QM$ 平行 $y$ 轴交 $BE$ 于 $M$,则 $M\left(x,\dfrac 13x-1\right)$,
则 $MQ=\dfrac 13x-1-\left(\dfrac 13x^2-3\right)=-\dfrac 13\left(x-\dfrac 12\right)^2+\dfrac{25}{12}$.
所以 $x=-\dfrac 12$ 时 $MQ$ 最大值为 $\dfrac {25}{12}$.
所以 $S_{\triangle EBQ \text{最大} }=S_{\triangle EQM}+S_{\triangle BQM}=\dfrac 12\left(x_B-x_E\right)\times \dfrac{25}{12}=\dfrac{125}{24}$.
同理可得,$Q$ 在 $C_2$ 上时,最大面积为 $\dfrac{45}{8}$.
综上最大面积为 $\dfrac {45}{8}$.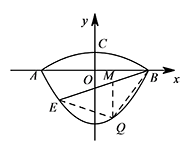
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2