如图，在平面直角坐标系 $xOy$ 中，抛物线 $y=ax^2+bx-3$（$a\ne 0$）与 $x$ 轴交于 $A\left(-2,0\right),B\left(4,0\right)$ 两点，与 $y$ 轴交于点 $C$．
【难度】
【出处】
无
【标注】
-
求抛物线解析式；标注答案$y=\dfrac 38x^2-\dfrac 34x-3$解析因为抛物线与 $x$ 轴交于 $A\left(-2,0\right),B\left(4,0\right)$ 两点，
所以 $y=a\left(x+2\right)\left(x-4\right)$．
所以 $-8a=-3$，解得 $a=\dfrac 38$．
抛物线解析式为 $y=\dfrac 38x^2-\dfrac 34x-3$． -
点 $P$ 从点 $A$ 出发，在线段 $AB$ 上以每秒 $3$ 个单位长度的速度向点 $B$ 运动，同时点 $Q$ 从点 $B$ 出发，在线段 $BC$ 上以每秒 $1$ 个单位长度的速度向点 $C$ 运动，其中一个点到达终点时，另一个点也停止运动，当 $\triangle PBQ$ 存在时，求运动多少秒时 $\triangle PBQ$ 的面积最大，最大面积是多少？标注答案当 $t=1$ 时，$\triangle PBQ$ 的面积最大，最大面积是 $\dfrac{9}{10}$解析如图，过点 $Q$ 作 $QH\perp x$ 轴，垂足为 $H$．
在 ${ \mathrm {Rt}}\triangle BCO$ 中，$OB=4$，$OC=3$，
所以 $BC=5$，$\sin B=\dfrac 35$．
在 ${\mathrm {Rt}}\triangle BQH$ 中，$BQ=t$，
所以 $QH=BQ\sin B =\dfrac 35t$．
所以 $S_{\triangle PBQ}=\dfrac 12BP\cdot QH=\dfrac 12\left(6-3t\right)\times \dfrac 35t =-\dfrac{9}{10}\left(t-1\right)^2+\dfrac{9}{10}$．
因为 $0\leqslant t\leqslant 2$，
所以当 $t=1$ 时，$\triangle PBQ$ 的面积最大，最大面积是 $\dfrac{9}{10}$． -
当 $\triangle PBQ$ 的面积最大时，在 $BC$ 下方的抛物线上是否存在点 $K$，使 $S_{\triangle CBK}:S_{\triangle PBQ}=5:2$，求点 $K$ 的坐标，若不存在，请说明理由．标注答案点 $K$ 的坐标为 $\left(1,-\dfrac{27}{8}\right)$ 或 $\left(3,-\dfrac{15}{8}\right)$解析
解法一 【等比转化法】当 $\triangle PBQ$ 的面积最大时，$t=1$，
此时 $P$ 是 $AB$ 的中点，$P\left(1,0\right)$，$BQ=1$．
如图，因为 $\triangle PBC$ 与 $\triangle PBQ$ 是同高三角形，
所以 $S_{\triangle PBC}:S_{\triangle PBQ}=BC:BQ=5:1$．
当 $S_{\triangle CBK}:S_{\triangle PBQ}=5:2$ 时，$S_{\triangle PBC}:S_{\triangle CBK}=2:1$．
因为 $\triangle PBC$ 与 $\triangle CBK$ 是同底三角形，所以对应高的比是 $2:1$．
如图，过 $x$ 轴上点 $B$ 的右侧取一点 $D$，使得 $BD=\dfrac 12 BP$，则 $D(\dfrac {11}2,0)$，过点 $D$ 作 $BC$ 的平行线交抛物线于 $K$，过点 $K$ 作 $KE\perp x$ 轴于 $E$．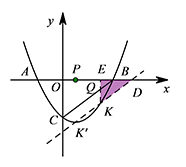
设点 $K$ 的坐标为 $\left(x,\dfrac 38\left(x+2\right)\left(x-4\right)\right)$．
由 $\dfrac{KE}{DE}=\dfrac{CO}{BO}$，得 $\dfrac{-\dfrac 38\left(x+2\right)\left(x-4\right)}{\dfrac{11}{2}-x}=\dfrac 34$．
整理得 $x^2-4x+3=0$．
解得 $x=1$ 或 $x=3$．
所以点 $K$ 的坐标为 $\left(1,-\dfrac{27}{8}\right)$ 或 $\left(3,-\dfrac{15}{8}\right)$．解法二 【铅锤法】由 $S_{\triangle CBK}:S_{\triangle PBQ}=5:2$，$S_{\triangle PBQ}=\dfrac{9}{10}$，
得 $S_{\triangle CBK}=\dfrac 94$．
如图，过点 $K$ 作 $x$ 轴的垂线交 $BC$ 于 $F$，
设点 $K$ 的坐标为 $\left(x,\dfrac 38x^2-\dfrac 34x-3\right)$．
由于点 $F$ 在直线 $BC$ 上，所以点 $F$ 的坐标为 $\left(x,\dfrac 34x-3\right)$．
所以 $KF =\left(\dfrac 34x-3\right)-\left(\dfrac 38x^2-\dfrac 34x-3\right)=-\dfrac 38x^2+\dfrac 32x$．
$\triangle CBK$ 被 $KF$ 分割为 $\triangle CKF$ 和 $\triangle BKF$，它们以 $FK$ 为底的高的和为 $OB=4$．
所以 $S_{\triangle CBK}=\dfrac 12\times4\left(-\dfrac 38x^2+\dfrac 32x\right)=\dfrac 94$．
解得 $x=1$ 或 $x=3$．
所以点 $K$ 的坐标为 $\left(1,-\dfrac{27}{8}\right)$ 或 $\left(3,-\dfrac{15}{8}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
