如图,在平面直角坐标系 $xOy$ 中,圆 $O:x^2+y^2=4$ 与 $x$ 轴的正半轴交于点 $A$,以 $A$ 为圆心的圆 $A:(x-2)^2+y^2=r^2(r>0)$ 与圆 $O$ 交于 $B,C$ 两点.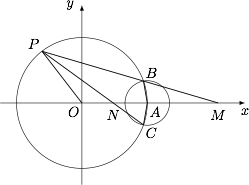

【难度】
【出处】
2015年全国高中数学联赛陕西省预赛(二试)
【标注】
-
求 $\overrightarrow{AB}\cdot\overrightarrow{AC}$ 的最小值;标注答案$-2$解析由对称性,设 $B(x_0,y_0),C(x_0,-y_0)$,则$$x_0^2+y_0^2=4,$$所以$$\overrightarrow{AB}\cdot\overrightarrow{AC}=(x_0-2)^2-y_0^2=2(x_0-1)^2-2.$$因为$$-2<x_0<2,$$所以当 $x_0=1$ 时,$\overrightarrow{AB}\cdot\overrightarrow{AC}$ 取得最小值为 $-2$.
-
设 $P$ 是圆 $O$ 上异于 $B,C$ 的任一点,直线 $PB,PC$ 与 $x$ 轴分别交于点 $M,N$,求 $S_{\triangle POM}\cdot S_{\triangle PON}$ 的最大值.标注答案$4$解析设 $P(x_1,y_1)$($y_1\ne \pm y_0$),则$$x_1^2+y_1^2=4.$$直线 $PB,PC$ 的方程为\[\begin{split}&PB:y-y_1=\dfrac{y_0-y_1}{x_0-x_1}(x-x_1),\\&PC:y-y_1=\dfrac{-y_0-y_1}{x_0-x_1}(x-x_1),\end{split}\]分别令 $y=0$,得$$x_M=\dfrac{x_1y_0-x_0y_1}{y_0-y_1},x_N=\dfrac{x_1y_0+x_0y_1}{y_0+y_1},$$所以$$x_M\cdot x_N=\dfrac{x_1^2y_0^2-x_0^2y_1^2}{y_0^2-y_1^2}=4,$$于是$$S_{\triangle POM}\cdot S_{\triangle PON}=\dfrac14|OM|\cdot|ON|\cdot y_1^2=y_1^2.$$因为$$-2\leqslant y_1\leqslant2,$$所以当 $y_1=2$ 或 $y_1=-2$ 时,$S_{\triangle POM}\cdot S_{\triangle PON}$ 取得最大值为 $4$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2