四边形 $ABCD$ 是边长为 $4$ 的正方形，点 $E$ 在边 $AD$ 所在的直线上，连接 $CE$，以 $CE$ 为边，作正方形 $CEFG$（点 $D$，点 $F$ 在直线 $CE$ 的同侧），连接 $BF$，当点 $E$ 在线段 $AD$ 上时，$AE=1$，求 $BF$ 的长．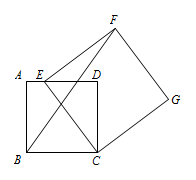
【难度】
【出处】
无
【标注】
【答案】
$BF=\sqrt{FK^2+BK^2}=\sqrt{74}$
【解析】
过点 $F$ 作 $FH\perp AD$ 交 $AD$ 的延长线于点 $H$，延长 $FH$ 交 $BC$ 的延长线于点 $K$，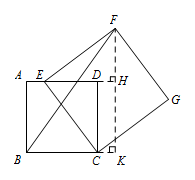
因为四边形 $CEFG$ 是正方形，四边形 $ABCD$ 是正方形，
根据“弦图模型”可得 $\angle ADC=90^\circ$，
$\angle DEC+\angle ECD=90^\circ$，
所以 $\angle ECD=\angle FEH$．
又因为 $\angle EDC=\angle FHE=90^\circ$，
所以 $\triangle ECD\cong \triangle FEH$，
所以 $FH=ED$．
因为 $AD=4,AE=1$，
所以 $ED=AD-AE=3$，
所以 $FH=3$．
因为 $CDHK$ 为矩形，
所以 $HK=CD=4$，
所以 $FK=FH+HK=7$．
因为 $\triangle ECD\cong \triangle FEH$，
所以 $EH=CD=AD=4$，
所以 $AE=DH=CK=1$，
所以 $BK=BC+CK=5$，
所以 $BF=\sqrt{FK^2+BK^2}=\sqrt{74}$．
因为四边形 $CEFG$ 是正方形，四边形 $ABCD$ 是正方形，根据“弦图模型”可得 $\angle ADC=90^\circ$，
$\angle DEC+\angle ECD=90^\circ$，
所以 $\angle ECD=\angle FEH$．
又因为 $\angle EDC=\angle FHE=90^\circ$，
所以 $\triangle ECD\cong \triangle FEH$，
所以 $FH=ED$．
因为 $AD=4,AE=1$，
所以 $ED=AD-AE=3$，
所以 $FH=3$．
因为 $CDHK$ 为矩形，
所以 $HK=CD=4$，
所以 $FK=FH+HK=7$．
因为 $\triangle ECD\cong \triangle FEH$，
所以 $EH=CD=AD=4$，
所以 $AE=DH=CK=1$，
所以 $BK=BC+CK=5$，
所以 $BF=\sqrt{FK^2+BK^2}=\sqrt{74}$．
答案
解析
备注
