如图，在锐角 $\triangle ABC$ 中，$AB=AC$，$\angle ACB$ 的平分线交 $AB$ 于点 $D$，过 $\triangle ABC$ 的外心 $O$ 作 $CD$ 的垂线交 $AC$ 于点 $E$，过点 $E$ 作 $AB$ 的平行线交 $CD$ 于点 $F$．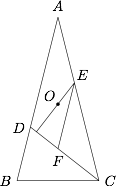
【难度】
【出处】
2010年全国高中数学联赛福建省预赛
【标注】
-
求证：$C$，$E$，$O$，$F$ 四点共圆；标注答案略解析连结 $OC$，$OA$，$OF$．
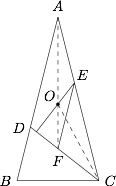因为 $AB=AC$，$O$ 为 $\triangle ABC$ 的外心，所以 $OA$ 平分 $\angle BAC$．
又因为 $OA=OC$，所以\[\begin{split}\angle OCA&=\angle OAC=\dfrac 12 \angle BAC\\&=\dfrac 12(180^{\circ}-2\angle B )\\&=90^{\circ}-\angle B.\end{split}\]因为 $OE \perp CD$，$CD$ 平分 $\angle ACB$，所以\[\begin{split}\angle OEC &=90^{\circ }-\angle ECD \\&=90^{\circ }-\dfrac 12\angle ACB\\&=90^{\circ }-\dfrac 12\angle B,\end{split}\]于是\[\begin{split}\angle EOC &=180^{\circ }-\angle OEC-\angle OCE \\&=180^{\circ }-\left(90^{\circ }-\dfrac 12\angle B\right)-(90^{\circ }- \angle B)\\&= \dfrac 32\angle B.\end{split}\]因为 $EF \parallel AD$，$CD$ 平分 $\angle ACB$，所以$$\angle CFE=\angle CDA=\angle ABC+\angle DCB=\dfrac 32\angle B,$$故$$\angle CFE=\angle EOC,$$因此 $C$，$E$，$O$，$F$ 四点共圆． -
求证：$A$，$O$，$F$ 三点共线；标注答案略解析由 $O$ 为 $\triangle ABC$ 的外心知，$$\angle AOC =2\angle B.$$由 $C$，$E$，$O$，$F$ 四点共圆知，$$\angle FOC=\angle FEC=\angle BAC,$$所以$$\angle FOC+\angle AOC=\angle BAC+2\angle B=180^{\circ},$$因此 $A$，$O$，$F$ 三点共线．
-
求证：$EA=EF$．标注答案略解析由 $C$，$E$，$O$，$F$ 四点共圆知，$$\angle OFE=\angle OCE=\angle OAC,$$所以 $EA=EF$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
