如图，圆内接四边形 $ABCD$ 中，边 $BA,CD$ 的延长线交于点 $P$，点 $O_{1},O_{2}$ 分别是 $\triangle ABC,\triangle DBC$ 的内心，直线 $BO_{1},CO_{2}$ 交于点 $H$．求证：$PH\perp O_{1}O_{2}$．
【难度】
【出处】
2016年全国高中数学联赛江苏省复赛（加试）
【标注】
【答案】
略
【解析】
如图，设直线 $O_{1}O_{2}$ 分别交 $AB,CD$ 于点 $E,F$，连接 $O_{1}C,O_{2}B$．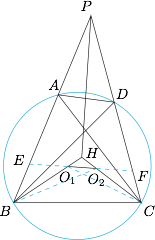
因为 $O_{1}$ 是 $\triangle ABC$ 的内心，所以\[\angle BO_{1}C=180^{\circ}-\dfrac{1}{2}(\angle ABC+\angle ACB)=90^{\circ}+\dfrac{1}{2}\angle BAC.\]同理$$\angle BO_{2}C=90^{\circ}+\dfrac{1}{2}\angle BDC.$$又因为 $\angle BAC=\angle BDC$，所以$$\angle BO_{1}C=\angle BO_{2}C,$$于是 $B,O_{1},O_{2},C$ 四点共圆，所以\[\begin{split}\angle EO_{1}B=\angle O_{2}CB =\dfrac{1}{2}\angle DCB,\\ \angle FO_{2}C=\angle O_{1}BC =\dfrac{1}{2}\angle ABC,\end{split}\]从而\[\begin{split}&\angle PEF=\angle EO_{1}B+\dfrac{1}{2}\angle ABC=\dfrac{1}{2}\angle DCB+\dfrac{1}{2}\angle ABC,\\ &\angle PFE=\angle FO_{2}C+\dfrac{1}{2}\angle DCB=\dfrac{1}{2}\angle ABC+\dfrac{1}{2}\angle DCB ,\end{split}\]所以 $\angle PEF=\angle PFE$，于是$$PE=PF,$$即 $\triangle PEF$ 为等腰三角形．
又因为点 $H$ 在 $\angle PBC$，$\angle PCB$ 的角平分线上，所以点 $H$ 是 $\triangle PBC$ 的内心，故 $PH\perp EF$，即 $PH\perp O_{1}O_{2}$．
因为 $O_{1}$ 是 $\triangle ABC$ 的内心，所以\[\angle BO_{1}C=180^{\circ}-\dfrac{1}{2}(\angle ABC+\angle ACB)=90^{\circ}+\dfrac{1}{2}\angle BAC.\]同理$$\angle BO_{2}C=90^{\circ}+\dfrac{1}{2}\angle BDC.$$又因为 $\angle BAC=\angle BDC$，所以$$\angle BO_{1}C=\angle BO_{2}C,$$于是 $B,O_{1},O_{2},C$ 四点共圆，所以\[\begin{split}\angle EO_{1}B=\angle O_{2}CB =\dfrac{1}{2}\angle DCB,\\ \angle FO_{2}C=\angle O_{1}BC =\dfrac{1}{2}\angle ABC,\end{split}\]从而\[\begin{split}&\angle PEF=\angle EO_{1}B+\dfrac{1}{2}\angle ABC=\dfrac{1}{2}\angle DCB+\dfrac{1}{2}\angle ABC,\\ &\angle PFE=\angle FO_{2}C+\dfrac{1}{2}\angle DCB=\dfrac{1}{2}\angle ABC+\dfrac{1}{2}\angle DCB ,\end{split}\]所以 $\angle PEF=\angle PFE$，于是$$PE=PF,$$即 $\triangle PEF$ 为等腰三角形．又因为点 $H$ 在 $\angle PBC$，$\angle PCB$ 的角平分线上，所以点 $H$ 是 $\triangle PBC$ 的内心，故 $PH\perp EF$，即 $PH\perp O_{1}O_{2}$．
答案
解析
备注
