如图,$\odot O$ 的一条弦 $AB$ 将圆分成两部分,$M$,$N$ 分别是两段弧的中点,以点 $B$ 为旋转中心,将弓形 $AMB$ 顺时针旋转一个角度成弓形 $A_1MB$,若 $AA_1$ 的中点为 $P$,$MN$ 的中点为 $Q$.求证:$MN=2PQ$.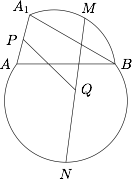

【难度】
【出处】
2010年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
设 $AB$,$A_1B$ 的中点分别为 $E$,$F$,由于在 $\odot O$ 中,点 $E$,$F$ 是重合的,且是直径 $MN$ 与 $AB$ 的交点,所以$$MF \cdot EN=AE \cdot EB=PE \cdot PF,$$则 $\dfrac {MF}{PF}=\dfrac {PE}{NE}$,且$$\angle MFP=\angle PEN=90^{\circ}+\angle ABA_1,$$于是 $\triangle MFP \sim \triangle PEN$,所以\[\begin{split} \angle MPN&=\angle MPF+\angle FPE+\angle EPN\\&=\angle MPF+\angle PFA_1+\angle PMF\\&=180^{\circ}-\angle MFA_1=90^{\circ} .\end{split}\]即点 $Q$ 为直角三角形 $MPN$ 的斜边中点,故 $MN=2PQ$.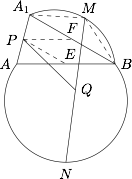

答案
解析
备注