如图，已知 $PA,PB$ 是 $\odot O$ 的两条切线，$PCD$ 是 $\odot O$ 的一条割线，$E$ 是 $AB$ 与 $PD$ 的交点．证明：$\dfrac{PC}{PD}=\dfrac{CE}{DE}$．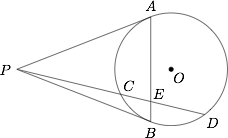
【难度】
【出处】
2009年全国高中数学联赛四川省预赛
【标注】
【答案】
略
【解析】
连结 $AC,AD,BC,BD$，则$$\dfrac{PC}{PD}=\dfrac{S_{\triangle{PAC}}}{S_{\triangle{PAD}}}=\dfrac{S_{\triangle{PBC}}}{S_{\triangle{PBD}}}.$$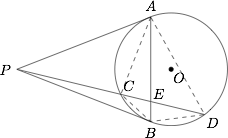
因为 $\triangle{PAC}\backsim \triangle{PDA}$，$\triangle{PBC}\backsim \triangle{PDB}$，所以$$\dfrac{S_{\triangle{PAC}}}{S_{\triangle{PAD}}}=\dfrac{AC^2}{AD^2},\dfrac{S_{\triangle{PBC}}}{S_{\triangle{PBD}}}=\dfrac{BC^2}{BD^2},$$故$$\dfrac{AC}{AD}=\dfrac{BC}{BD},$$于是$$\dfrac{PC}{PD}=\dfrac{AC^2}{AD^2}=\dfrac{AC}{AD}\cdot \dfrac{BC}{BD}.\cdots \text{ ① }$$又因为 $\triangle{ACE}\backsim \triangle{DBE}$，$\triangle{BCE}\backsim \triangle{DAE}$，所以\[\begin{split}&\dfrac{AC}{DB}=\dfrac{AE}{DE}\cdots \text{ ② }\\ & \dfrac{BC}{DA}=\dfrac{CE}{AE}\cdots \text{ ③ }\end{split}\]由 ①，②，③ 得 $\dfrac{PC}{PD}=\dfrac{CE}{DE}$．
因为 $\triangle{PAC}\backsim \triangle{PDA}$，$\triangle{PBC}\backsim \triangle{PDB}$，所以$$\dfrac{S_{\triangle{PAC}}}{S_{\triangle{PAD}}}=\dfrac{AC^2}{AD^2},\dfrac{S_{\triangle{PBC}}}{S_{\triangle{PBD}}}=\dfrac{BC^2}{BD^2},$$故$$\dfrac{AC}{AD}=\dfrac{BC}{BD},$$于是$$\dfrac{PC}{PD}=\dfrac{AC^2}{AD^2}=\dfrac{AC}{AD}\cdot \dfrac{BC}{BD}.\cdots \text{ ① }$$又因为 $\triangle{ACE}\backsim \triangle{DBE}$，$\triangle{BCE}\backsim \triangle{DAE}$，所以\[\begin{split}&\dfrac{AC}{DB}=\dfrac{AE}{DE}\cdots \text{ ② }\\ & \dfrac{BC}{DA}=\dfrac{CE}{AE}\cdots \text{ ③ }\end{split}\]由 ①，②，③ 得 $\dfrac{PC}{PD}=\dfrac{CE}{DE}$．
答案
解析
备注
