已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$），$A_d$ 为与原点距离等于 $d$ 的直线全体所成的集合．是否存在常数 $d(0<d<b)$，使得对任意的 $l\in A_d$，均存在 $l_1,l_2\in A_d$，$l_1,l_2$ 分别过 $l$ 与椭圆 $E$ 的交点 $P,Q$，且有 $l_1\parallel l_2$？说明理由．
【难度】
【出处】
2012年全国高中数学联赛吉林省预赛
【标注】
【答案】
存在唯一的 $d=\dfrac{ab}{\sqrt{a^2+b^2}}$ 符合题意
【解析】
假设这样的常数 $d$ 存在．
先从特殊情况入手，取 $l\in A_d$ 为特殊直线：$x=d$，且和椭圆交于两点 $P,Q$．
作与原点 $O$ 为圆心，$d$ 为半径的圆 $O_d$ 交 $x$ 轴的正半轴于点 $G$．
显然圆 $O_d$ 与直线 $PQ$ 切于点 $G$，且 $GP=GQ$．
依题意，存在直线 $l_1,l_2$，分别过点 $P$ 和 $Q$，且与圆 $O_d$ 相切，设切点分别为 $P_0,Q_0$，则 $OP_0,OQ_0$ 分别垂直互相平行的直线 $l_1,l_2$，所以 $P_0Q_0$ 为圆 $O_d$ 的直径，则 $OG$ 是梯形 $P_0Q_0QP$ 的中位线．
由 $OG\perp PQ$ 知$$l_1\perp PQ,l_2\perp PQ,$$因此 $P$ 点的坐标为 $(d,d)$，且 $l_1,l_2$ 分别为 $y=d$ 和 $y=-d$．
因为 $P(d,d)$ 位于椭圆上，若这样的常数 $d$ 存在，由椭圆方程可得$$\dfrac{d^2}{a^2}+\dfrac{d^2}{b^2}=1,$$解得 $d=\dfrac{ab}{\sqrt{a^2+b^2}}$．
下证：$d=\dfrac{ab}{\sqrt{a^2+b^2}}$ 即为所求．
先证若 $l\in A_d$，且和椭圆交于两点 $P,Q$，则必有 $OP\perp OQ$．
设直线 $l$ 的方程为 $y=kx+m$，则原点 $O$ 到直线 $l$ 的距离为 $\dfrac{|m|}{\sqrt{k^2+1}}$，从而有$$\dfrac{ab}{\sqrt{a^2+b^2}}=\dfrac{|m|}{\sqrt{k^2+1}},$$即$$(k^2+1)a^2b^2=m^2(a^2+b^2).$$将直线 $l$ 的方程 $y=kx+m$ 代入椭圆方程得$$(a^2k^2+b^2)x^2+2a^2kmx+a^2(m^2-b^2)=0,$$设 $P(x_1,y_1),Q(x_2,y_2)$，则由韦达定理得$$x_1+x_2=-\dfrac{2a^2km}{a^2k^2+b^2},x_1x_2=\dfrac{a^2(m^2-b^2)}{a^2k^2+b^2},$$从而有\[\begin{split}x_1x_2+y_1y_2&=x_1x_2+(kx_1+m)(kx_2+m)\\&=(k^2+1)x_1x_2+mk(x_1+x_2)+m^2\\&=\dfrac{(a^2+b^2)m^2-(k^2+1)a^2b^2}{a^2k^2+b^2}\\&=0,\end{split}\]即 $OP\perp OQ$．
易证若直线 $l\in A_d$ 的斜率不存在，$OP\perp OQ$．
假设 $l_1$ 和椭圆交于 $P,P_1$，$l_2$ 和椭圆交于 $Q,Q_1$，如图所示．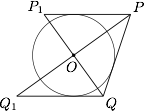
则有$$OP\perp OQ,OP\perp OP_1,OQ\perp OQ_1,$$并且有$$\angle OPP_1=\angle OPQ,\angle OQQ_1=\angle OQP,$$因此 $\angle PP_1Q+\angle Q_1QP=\pi$，即 $l_1,l_2$ 平行．
综上所述，存在唯一的 $d=\dfrac{ab}{\sqrt{a^2+b^2}}$，使得对任意的 $l\in A_d$，均存在符合题意的 $l_1,l_2\in A_d$．
先从特殊情况入手，取 $l\in A_d$ 为特殊直线：$x=d$，且和椭圆交于两点 $P,Q$．
作与原点 $O$ 为圆心，$d$ 为半径的圆 $O_d$ 交 $x$ 轴的正半轴于点 $G$．
显然圆 $O_d$ 与直线 $PQ$ 切于点 $G$，且 $GP=GQ$．
依题意，存在直线 $l_1,l_2$，分别过点 $P$ 和 $Q$，且与圆 $O_d$ 相切，设切点分别为 $P_0,Q_0$，则 $OP_0,OQ_0$ 分别垂直互相平行的直线 $l_1,l_2$，所以 $P_0Q_0$ 为圆 $O_d$ 的直径，则 $OG$ 是梯形 $P_0Q_0QP$ 的中位线．
由 $OG\perp PQ$ 知$$l_1\perp PQ,l_2\perp PQ,$$因此 $P$ 点的坐标为 $(d,d)$，且 $l_1,l_2$ 分别为 $y=d$ 和 $y=-d$．
因为 $P(d,d)$ 位于椭圆上，若这样的常数 $d$ 存在，由椭圆方程可得$$\dfrac{d^2}{a^2}+\dfrac{d^2}{b^2}=1,$$解得 $d=\dfrac{ab}{\sqrt{a^2+b^2}}$．
下证：$d=\dfrac{ab}{\sqrt{a^2+b^2}}$ 即为所求．
先证若 $l\in A_d$，且和椭圆交于两点 $P,Q$，则必有 $OP\perp OQ$．
设直线 $l$ 的方程为 $y=kx+m$，则原点 $O$ 到直线 $l$ 的距离为 $\dfrac{|m|}{\sqrt{k^2+1}}$，从而有$$\dfrac{ab}{\sqrt{a^2+b^2}}=\dfrac{|m|}{\sqrt{k^2+1}},$$即$$(k^2+1)a^2b^2=m^2(a^2+b^2).$$将直线 $l$ 的方程 $y=kx+m$ 代入椭圆方程得$$(a^2k^2+b^2)x^2+2a^2kmx+a^2(m^2-b^2)=0,$$设 $P(x_1,y_1),Q(x_2,y_2)$，则由韦达定理得$$x_1+x_2=-\dfrac{2a^2km}{a^2k^2+b^2},x_1x_2=\dfrac{a^2(m^2-b^2)}{a^2k^2+b^2},$$从而有\[\begin{split}x_1x_2+y_1y_2&=x_1x_2+(kx_1+m)(kx_2+m)\\&=(k^2+1)x_1x_2+mk(x_1+x_2)+m^2\\&=\dfrac{(a^2+b^2)m^2-(k^2+1)a^2b^2}{a^2k^2+b^2}\\&=0,\end{split}\]即 $OP\perp OQ$．
易证若直线 $l\in A_d$ 的斜率不存在，$OP\perp OQ$．
假设 $l_1$ 和椭圆交于 $P,P_1$，$l_2$ 和椭圆交于 $Q,Q_1$，如图所示．
则有$$OP\perp OQ,OP\perp OP_1,OQ\perp OQ_1,$$并且有$$\angle OPP_1=\angle OPQ,\angle OQQ_1=\angle OQP,$$因此 $\angle PP_1Q+\angle Q_1QP=\pi$，即 $l_1,l_2$ 平行．综上所述，存在唯一的 $d=\dfrac{ab}{\sqrt{a^2+b^2}}$，使得对任意的 $l\in A_d$，均存在符合题意的 $l_1,l_2\in A_d$．
答案
解析
备注
