如图，$\triangle ABC$ 中，$AB>AC$，点 $D,E$ 分别在边 $AB,AC$ 上，且 $BD=CE$．$\angle BAC$ 的外角平分线与 $\triangle ADE$ 的外接圆交于 $A,P$ 两点．求证：$A,P,B,C$ 四点共圆．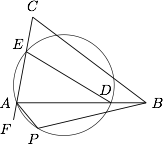
【难度】
【出处】
2015年全国高中数学联赛江苏省初赛
【标注】
【答案】
略
【解析】
如图，连接 $PD,PE,PC$．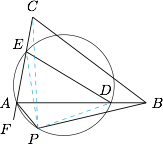
因为四边形 $APDE$ 是圆内接四边形，所以$$\angle PAD=\angle PED,\angle PAF=\angle PDE,$$又因为 $AP$ 是 $\angle BAC$ 的外角平分线，所以 $\angle PAD=\angle PAF$，从而$$\angle PED=\angle PDE,$$故 $PD=PE$．
又因为 $\angle ADP=\angle AEP$，所以 $\angle BDP=\angle CEP$．
又因为 $BD=CE$，所以$$\triangle BDP\cong\triangle CEP,$$从而 $\angle PBD=\angle PCE$，即$$\angle PBA=\angle PCA,$$所以 $A,P,B,C$ 四点共圆．
因为四边形 $APDE$ 是圆内接四边形，所以$$\angle PAD=\angle PED,\angle PAF=\angle PDE,$$又因为 $AP$ 是 $\angle BAC$ 的外角平分线，所以 $\angle PAD=\angle PAF$，从而$$\angle PED=\angle PDE,$$故 $PD=PE$．又因为 $\angle ADP=\angle AEP$，所以 $\angle BDP=\angle CEP$．
又因为 $BD=CE$，所以$$\triangle BDP\cong\triangle CEP,$$从而 $\angle PBD=\angle PCE$，即$$\angle PBA=\angle PCA,$$所以 $A,P,B,C$ 四点共圆．
答案
解析
备注
