已知点 $O$ 是正方形 $ABCD$ 对角线 $BD$ 的中点，
【难度】
【出处】
无
【标注】
-
如图1，若点 $E$ 是 $OD$ 的中点，点 $F$ 是 $AB$ 上一点，且使得 $\angle CEF=90^\circ$，过点 $E$ 作 $ME\parallel AD$，交 $AB$ 于点 $M$，交 $CD$ 于点 $N$，
① $\angle AEM=\angle FEM$；
② 点 $F$ 是 $AB$ 的中点；标注答案略解析① 过点 $E$ 作 $EG\perp BC$，垂足为点 $G$，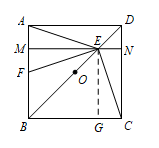
则四边形 $MBGE$ 为正方形，$ME=GE$，$\angle MFG=90^\circ$，即 $\angle MEF+\angle FEG=90^\circ$，
又 $\angle CEG+\angle FEG=90^\circ$，
所以 $\angle CEG=\angle FEM$．
又因为 $GE=ME,\angle EGC=\angle EMF=90^\circ$，
所以 $\triangle CEG\cong \triangle FEM$，
所以 $CE=EF$．
又因为四边形 $ABCD$ 是正方形，
所以 $AB=CB,\angle ABE=\angle CBE=45^\circ,BE=BE$，
所以 $\triangle ABE\cong \triangle CBE$，
所以 $AE=FE$．
又因为 $EM\perp AB$，
所以 $\angle AEM=\angle FEM$．
② 设 $AM=x$，
因为 $AE=EF,EM\perp AB$，
所以 $AM=FM=x$，$AF=2x$，$DN=AM=x$．
因为 $\angle ADB=45^\circ$，
所以 $DE=\sqrt 2DN=\sqrt 2 x,BD=2OD=2\sqrt 2 x,BD=2DO=4\sqrt 2 x$．
因为 $\angle ADB=45^\circ$，
所以 $AB=BD\cdot \sin 45^\circ=4x$．
又因为 $AF=2x$，所以 $AF=\dfrac 12AB$，
所以点 $F$ 是 $AB$ 的中点． -
如图2，若点 $E$ 是 $OD$ 上一点，点 $F$ 是 $AB$ 上一点，且使 $\dfrac{DE}{DO}=\dfrac{AF}{AB}=\dfrac 13$，请判断 $\triangle EFC$ 的形状，并说明理由；标注答案$\triangle EFC$ 是等腰直角三角形解析过点 $E$ 作 $EM\perp AB$ 垂足为点 $M$，延长 $ME$ 交 $CD$ 于点 $N$，过点 $E$ 作 $EG\perp BC$ 垂足为 $G$，
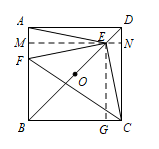所以 $\triangle AEM\cong \triangle CEG$，
所以 $\angle AEM=\angle CEG$，设 $AM=x$．
则 $DN=AM=x,DE=\sqrt 2x,DO=3DE=3\sqrt 2x,BD=2DO=6\sqrt 2 x$，
所以 $AB=6x$．
因为 $\dfrac{AF}{AB}=\dfrac 13$，
所以 $AF=2x$．
又因为 $AM=x$，
所以 $AM=MF=x$，
所以 $\triangle AME\cong \triangle FME$，
所以 $AE=EF,\angle AEM=\angle FEM$．
又因为 $AE=CE,\angle AEM=\angle CEG$，
所以 $EF=CE,\angle FEM=\angle CEG$．
又因为 $\angle MEG=90^\circ$，
所以 $\angle MEF+\angle FEG=90^\circ$，
所以 $\angle CEG+\angle FEG=90^\circ$，即 $\angle CEF=90^\circ$．
又因为 $FE=CE$，
所以 $\triangle EFC$ 是等腰直角三角形． -
如图3，若 $E$ 是 $OD$ 上的动点（不与 $O,D$ 重合），连接 $CE$，过 $E$ 点作 $EF\perp CE$，交 $AB$ 于点 $F$，当 $\dfrac{DE}{DB}=\dfrac{m}{n}$ 时，请猜想 $\dfrac{AF}{AB}$ 的值（请直接写出结论）标注答案$\dfrac{AF}{AB}=\dfrac{2m}{n}$解析过点 $E$ 作 $EM\perp AB$，垂足为点 $M$，延长 $ME$ 交 $CD$ 于点 $N$，过点 $E$ 作 $EG\perp BA$ 垂足为点 $G$，
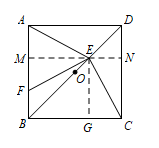则 $\triangle AEM\cong \triangle CEG$，
所以 $\angle AEM=\angle CEG$．
因为 $\angle FEC=90^\circ$，
所以 $angle CEG+\angle FEG=90^\circ$．
又因为 $\angle MEG=90^\circ$，
所以 $\angle MEF+\angle FEG=90^\circ,\angle CEG=\angle MEF$．
因为 $\angle MEG=90^\circ$，
所以 $\angle MEF+\angle FEG=90^\circ$，
所以 $\angle CEG=\angle MEF$．
因为 $\angle CEG=\angle AEF$，
所以 $\angle AEF=\angle MEF$，
所以 $\triangle AEM\cong \triangle FEM$，
所以 $AM=FM$．
设 $AM=x$，
则 $AF=2x,DN=x,DE=\sqrt 2 x$，
所以 $BD=\dfrac nm\sqrt 2x$，
所以 $\dfrac{AF}{AB}=\dfrac{2m}{n}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
