如图,在平面直角坐标系 $xOy$ 中,圆 $O_1$,圆 $O_2$ 都与直线 $l:y=kx$ 及 $x$ 轴正半轴相切.若两圆的半径之积为 $2$,两圆的一个交点为 $P(2,2)$,求直线 $l$ 的方程.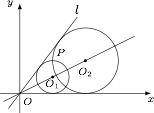

【难度】
【出处】
2015年全国高中数学联赛江苏省初赛
【标注】
【答案】
$y=\dfrac43x$
【解析】
由题意,圆心 $O_1,O_2$ 都在 $x$ 轴与直线 $l$ 的角平分线上.
若直线 $l$ 的斜率 $k=\tan\alpha$,设 $t=\tan\dfrac{\alpha}{2}$,则$$k=\dfrac{2t}{1-t^2}.$$因圆心 $O_1,O_2$ 在直线 $y=tx$ 上,可设 $O_1(m,mt),O_2(n,nt)$.
由于交点 $P(2,2)$ 在第一象限,所以$$m>0,n>0,t>0,$$故\[\begin{split}&\odot O_1:(x-m)^2+(y-mt)^2=(mt)^2,\\&\odot O_2:(x-n)^2+(y-nt)^2=(nt)^2,\end{split}\]因此有$$\begin{cases}(2-m)^2+(2-mt)^2=(mt)^2,\\(2-n)^2+(2-nt)^2=(nt)^2,\end{cases}$$整理得$$\begin{cases}m^2-(4+4t)m+8=0,\\n^2-(4+4t)n+8=0,\end{cases}$$所以 $m,n$ 是方程$$x^2-(4+4t)x+8=0$$的两根,从而$$mn=8.$$因为半径的积 $(mt)(nt)=2$,得 $t=\dfrac12$,所以$$k=\dfrac{2t}{1-t^2}=\dfrac43.$$因此,直线 $l$ 的方程为 $y=\dfrac43x$.
若直线 $l$ 的斜率 $k=\tan\alpha$,设 $t=\tan\dfrac{\alpha}{2}$,则$$k=\dfrac{2t}{1-t^2}.$$因圆心 $O_1,O_2$ 在直线 $y=tx$ 上,可设 $O_1(m,mt),O_2(n,nt)$.
由于交点 $P(2,2)$ 在第一象限,所以$$m>0,n>0,t>0,$$故\[\begin{split}&\odot O_1:(x-m)^2+(y-mt)^2=(mt)^2,\\&\odot O_2:(x-n)^2+(y-nt)^2=(nt)^2,\end{split}\]因此有$$\begin{cases}(2-m)^2+(2-mt)^2=(mt)^2,\\(2-n)^2+(2-nt)^2=(nt)^2,\end{cases}$$整理得$$\begin{cases}m^2-(4+4t)m+8=0,\\n^2-(4+4t)n+8=0,\end{cases}$$所以 $m,n$ 是方程$$x^2-(4+4t)x+8=0$$的两根,从而$$mn=8.$$因为半径的积 $(mt)(nt)=2$,得 $t=\dfrac12$,所以$$k=\dfrac{2t}{1-t^2}=\dfrac43.$$因此,直线 $l$ 的方程为 $y=\dfrac43x$.
答案
解析
备注