在如图所示的多面体 $ABCDEF$ 中，已知 $AD,BE,CF$ 都与平面 $ABC$ 垂直．设 $AD=a,BE=b,CF=c$，$AB=AC=BC=1$，求四面体 $ABCE$ 与 $BDEF$ 公共部分的体积（用 $a,b,c$ 表示）．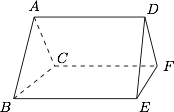
【难度】
【出处】
2015年全国高中数学联赛安徽省预赛
【标注】
【答案】
$\dfrac{\sqrt3b^3}{12(a+b)(b+c)}$
【解析】
如图．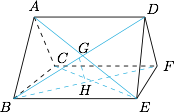
设 $AE\cap BD=G,BF\cap CE=H$，则四面体 $BEGH$ 是 $ABCE$ 与 $BDEF$ 的公共部分．
设 $H$ 到直线 $BC$ 的距离为 $d_1$，$G$ 到平面 $BCFE$ 的距离为 $d_2$，$A$ 到平面 $BCFE$ 的距离为 $d_3$，
因为$$\dfrac {CH}{HE}=\dfrac {CF}{BE}=\dfrac cb,$$所以$$\dfrac {d_1}{BE}=\dfrac {CH}{CE}=\dfrac {c}{b+c},$$故 $d_1=\dfrac {bc}{b+c}$，于是 $\triangle BEH$ 的面积为$$S=\dfrac{b-d_1}{2}=\dfrac {b^2}{2(b+c)}.$$因为 $d_3=\dfrac {\sqrt 3}{2}$，而$$\dfrac {d_2}{d_3}=\dfrac {GE}{AE}=\dfrac {b}{a+b},$$所以 $d_2=\dfrac {\sqrt 3b}{2(a+b)}$．
因此，所求体积为$$V_{BEGH}=\dfrac 13S\cdot d_2=\dfrac{\sqrt3b^3}{12(a+b)(b+c)}.$$
设 $AE\cap BD=G,BF\cap CE=H$，则四面体 $BEGH$ 是 $ABCE$ 与 $BDEF$ 的公共部分．设 $H$ 到直线 $BC$ 的距离为 $d_1$，$G$ 到平面 $BCFE$ 的距离为 $d_2$，$A$ 到平面 $BCFE$ 的距离为 $d_3$，
因为$$\dfrac {CH}{HE}=\dfrac {CF}{BE}=\dfrac cb,$$所以$$\dfrac {d_1}{BE}=\dfrac {CH}{CE}=\dfrac {c}{b+c},$$故 $d_1=\dfrac {bc}{b+c}$，于是 $\triangle BEH$ 的面积为$$S=\dfrac{b-d_1}{2}=\dfrac {b^2}{2(b+c)}.$$因为 $d_3=\dfrac {\sqrt 3}{2}$，而$$\dfrac {d_2}{d_3}=\dfrac {GE}{AE}=\dfrac {b}{a+b},$$所以 $d_2=\dfrac {\sqrt 3b}{2(a+b)}$．
因此，所求体积为$$V_{BEGH}=\dfrac 13S\cdot d_2=\dfrac{\sqrt3b^3}{12(a+b)(b+c)}.$$
答案
解析
备注
