在四边形 $ABCD$ 中，$AB\parallel DC$，$AF$ 与 $DC$ 的延长线交于点 $F$，$E$ 是 $BC$ 的中点，若 $AE$ 是 $\angle BAF$ 的平分线，试探究 $AB,AF,CF$ 之间的等量关系，并证明结论；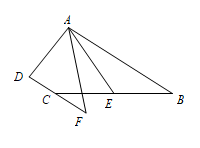
【难度】
【出处】
无
【标注】
【答案】
$AB=AF+CF$
【解析】
延长 $AE$ 交 $DF$ 的延长线于点 $G$，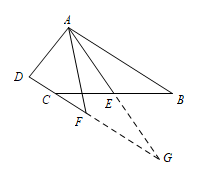
因为点 $E$ 是 $BC$ 的中点，
所以 $CE=BE$．
因为 $AB\parallel DC$，
所以 $\angle BAE=\angle G,\angle B=\angle ECG$，
所以 $\triangle ABE\cong \triangle GCE$，
所以 $AB=GC$．
又因为 $AE$ 平分 $\angle FAB$，
所以 $\angle BAE=\angle FAG$，
所以 $\angle G=\angle FAG$，
所以 $AF=FG$．
因为 $GC=FG+CF$，
所以 $AB=AF+CF$．
因为点 $E$ 是 $BC$ 的中点，所以 $CE=BE$．
因为 $AB\parallel DC$，
所以 $\angle BAE=\angle G,\angle B=\angle ECG$，
所以 $\triangle ABE\cong \triangle GCE$，
所以 $AB=GC$．
又因为 $AE$ 平分 $\angle FAB$，
所以 $\angle BAE=\angle FAG$，
所以 $\angle G=\angle FAG$，
所以 $AF=FG$．
因为 $GC=FG+CF$，
所以 $AB=AF+CF$．
答案
解析
备注
