在 $\rm{Rt}\triangle ABC$ 中，$\angle ACB=90^\circ$，$AC=BC$，点 $D,E$ 分别在 $AC,BC$ 边上，$DC=EC$，连接 $AE,AE,BD$，点 $M,N,P$ 分别是 $AE,BD,AB$ 的中点，连接 $PM,PN,MN$，将 $\triangle DEC$ 绕点 $C$ 逆时针旋转到如图位置，则探究 $BE,MN$ 的数量关系．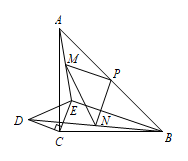
【难度】
【出处】
无
【标注】
【答案】
$BE=\sqrt 2 MN$
【解析】
连接 $AD$，延长 $BE$ 交 $AD$ 于点 $H$，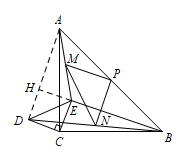
因为 $\triangle ABC$ 和 $\triangle CDE$ 是等腰直角三角形，
所以 $CD=CE,CA=CB,\angle ACB=\angle DCE=90^\circ$．
因为 $\angle ACB-\angle ACE=\angle DCE-\angle ACE$，
所以 $\angle ACD=\angle ECB$，
所以 $\triangle ECB\cong \triangle DCA$，
所以 $BE=AD,\angle DAC=\angle EBC$．
因为 $\angle AHB=180^\circ-(\angle HAB+\angle ABH)=90^\circ$，
所以 $BH\perp AD$．
因为 $M,N,P$ 分别为 $AE,BD,AB$ 的中点，
所以 $PM\parallel BE,PM=\dfrac 12 BE,PN\parallel AD,PN=\dfrac 12AD$，
所以 $PM=PN,\angle MPN=90^\circ$，
所以 $BE=2PM=\sqrt 2MN$．
因为 $\triangle ABC$ 和 $\triangle CDE$ 是等腰直角三角形，所以 $CD=CE,CA=CB,\angle ACB=\angle DCE=90^\circ$．
因为 $\angle ACB-\angle ACE=\angle DCE-\angle ACE$，
所以 $\angle ACD=\angle ECB$，
所以 $\triangle ECB\cong \triangle DCA$，
所以 $BE=AD,\angle DAC=\angle EBC$．
因为 $\angle AHB=180^\circ-(\angle HAB+\angle ABH)=90^\circ$，
所以 $BH\perp AD$．
因为 $M,N,P$ 分别为 $AE,BD,AB$ 的中点，
所以 $PM\parallel BE,PM=\dfrac 12 BE,PN\parallel AD,PN=\dfrac 12AD$，
所以 $PM=PN,\angle MPN=90^\circ$，
所以 $BE=2PM=\sqrt 2MN$．
答案
解析
备注
