在四面体 $ABCD$ 中,$AD\perp$ 平面 $BCD$,$\angle{ABD}=\angle{BDC}=\theta<45^{\circ}$.已知 $E$ 是 $BD$ 上一点,满足 $CE\perp BD$ 且 $BE=AD=1$.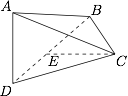

【难度】
【出处】
2011年全国高中数学联赛天津市预赛
【标注】
-
证明:$\angle{BAC}=\theta$;标注答案略解析因为 $AD=BE=1$,所以$$AB=\dfrac 1{\sin \theta},BD=\dfrac {\cos \theta}{\sin \theta},DE=\dfrac{\cos \theta}{\sin \theta}-1,$$以及$$CD=\dfrac{DE}{\cos \theta}=\dfrac 1{\sin \theta}-\dfrac 1{\cos \theta},$$进而得到$$\begin{split}AC&=\sqrt{AD^2+CD^2}\\ &=\sqrt{1+\left(\dfrac 1{\sin \theta}-\dfrac 1{\cos \theta}\right)^2}\\ &=\dfrac{1}{\sin \theta\cos \theta}-1.\end{split}$$设 $\angle{BAC}=\alpha$,分别在 $\triangle{ABC}$ 和 $\triangle{DBC}$ 中用余弦定理,有\[\begin{split}&BC^2=AB^2+AC^2-2AB\cdot AC\cdot \cos \alpha,\\&BC^2=BD^2+CD^2-2BD\cdot CD\cdot \cos \theta,\end{split}\]以上两式相减,并注意\[\begin{split}&AB^2=BD^2+AD^2,\\& AC^2=CD^2+AD^2,\end{split}\]则可得到$$2AD^2-2AB\cdot AC \cdot \cos \alpha +2BD\cdot CD \cdot \cos \theta=0,$$从而\[\begin{split}\cos \alpha &=\dfrac{AD^2+BD\cdot CD\cdot \cos \theta}{AB\cdot AC}\\&=\dfrac{1+\dfrac{\cos \theta}{\sin \theta}\cdot \left(\dfrac 1{\sin \theta}-\dfrac 1{\cos \theta}\right)\cdot \cos \theta}{\dfrac 1{\sin \theta}\cdot \left(\dfrac 1{\sin \theta \cos \theta}-1\right)}\\&=\cos \theta.\end{split}\]这就证明了 $\angle{BAC}=\theta$.
-
若点 $D$ 到平面 $ABC$ 的距离为 $\dfrac 4{13}$,求 $\cos{\theta}$ 的值.标注答案$\dfrac 45$解析注意四面体 $ABCD$ 的体积为$$V=\dfrac 13 AD\cdot S_{BCD}=\dfrac 16 AD\cdot BD\cdot CD\cdot \sin \theta,$$而 $\triangle{ABC}$ 的面积为$$S=\dfrac 12AB\cdot AC\cdot \sin \theta,$$因此,点 $D$ 到平面 $ABC$ 的距离为$$\dfrac{3V}{S}=\dfrac{AD\cdot BD \cdot CD}{AB\cdot AC}=\dfrac{\cos ^2 \theta-\cos \theta \sin \theta}{1-\sin \theta \cos \theta}.$$令上式等于 $\dfrac 4{13}$,解得 $\cos \theta =\dfrac 45$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2