已知 $O$ 为 $\triangle ABC$ 的外心，且 $\overrightarrow{OA}+\sqrt 3\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow 0$，则 $\angle AOC$ 为 \((\qquad)\)
【难度】
【出处】
2017年清华大学THUSSAT附加学科测试数学部分（二测）
【标注】
【答案】
C
【解析】
如图，$\overrightarrow{OD}=-2\overrightarrow{OC}$，$\overrightarrow{OB'}=\sqrt 3\overrightarrow{OB}$，连接 $B'D,AD$．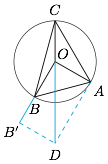
不妨设圆的半径为 $1$，则 $OB'=\sqrt 3$，$B'D=OA=1$，$OD=2$，于是四边形 $OB'DA$ 是矩形，且 $\angle DOA=60^\circ$，于是 $\angle AOC=120^\circ$．
不妨设圆的半径为 $1$，则 $OB'=\sqrt 3$，$B'D=OA=1$，$OD=2$，于是四边形 $OB'DA$ 是矩形，且 $\angle DOA=60^\circ$，于是 $\angle AOC=120^\circ$．
题目
答案
解析
备注
